- ROC曲线

ROC曲线
基本概念
阳性 (P, positive)阴性 (N, Negative)真阳性 (TP, true positive) 正确的肯定。又称:命中 (hit) 真阴性 (TN, true negative)正确的否定。又称:正确拒绝 (correct rejection) 伪阳性 (FP, false positive)错误的肯定,又称:假警报 (false alarm),第一型错误 伪阴性 (FN, false negative)错误的否定,又称:未命中 (miss),第二型错误 真阳性率 (TPR, true positive rate)又称:命中率 (hit rate)、敏感度(sensitivity) TPR = TP / P = TP / (TP+FN) 伪阳性率(FPR, false positive rate)又称:错误命中率,假警报率 (false alarm rate) FPR = FP / N = FP / (FP + TN) 准确度 (ACC, accuracy)ACC = (TP + TN) / (P + N) 即:(真阳性+真阴性) / 总样本数 真阴性率 (TNR)又称:特异度 (SPC, specificity) SPC = TN / N = TN / (FP + TN) = 1 - FPR 阳性预测值 (PPV)PPV = TP / (TP + FP) 阴性预测值 (NPV)NPV = TN / (TN + FN) 假发现率 (FDR)FDR = FP / (FP + TP) Matthews相关系数 (MCC),即 Phi相关系数F1 = 2TP/(P+P') |
| Source: Fawcett (2006). |
分类模型(又称分类器,或诊断)是将一个实例映射到一个特定类的过程。ROC分析的是二元分类模型,也就是输出结果只有两种类别的模型,例如:(阳性/阴性)(有病/没病)(垃圾邮件/非垃圾邮件)(敌军/非敌军)。
当讯号侦测(或变数测量)的结果是一个连续值时,类与类的边界必须用一个阈值(英语:threshold)来界定。举例来说,用血压值来检测一个人是否有高血压,测出的血压值是连续的实数(从0~200都有可能),以收缩压140/舒张压90为阈值,阈值以上便诊断为有高血压,阈值未满者诊断为无高血压。二元分类模型的个案预测有四种结局:
真阳性(TP):诊断为有,实际上也有高血压。
伪阳性(FP):诊断为有,实际却没有高血压。
真阴性(TN):诊断为没有,实际上也没有高血压。
伪阴性(FN):诊断为没有,实际却有高血压。
这四种结局可以画成2 × 2的混淆矩阵:
ROC空间
阳性 (P, positive)阴性 (N, Negative)真阳性 (TP, true positive) 正确的肯定。又称:命中 (hit) 真阴性 (TN, true negative)正确的否定。又称:正确拒绝 (correct rejection) 伪阳性 (FP, false positive)错误的肯定,又称:假警报 (false alarm),第一型错误 伪阴性 (FN, false negative)错误的否定,又称:未命中 (miss),第二型错误 真阳性率 (TPR, true positive rate)又称:命中率 (hit rate)、敏感度(sensitivity) TPR = TP / P = TP / (TP+FN) 伪阳性率(FPR, false positive rate)又称:错误命中率,假警报率 (false alarm rate) FPR = FP / N = FP / (FP + TN) 准确度 (ACC, accuracy)ACC = (TP + TN) / (P + N) 即:(真阳性+真阴性) / 总样本数 真阴性率 (TNR)又称:特异度 (SPC, specificity) SPC = TN / N = TN / (FP + TN) = 1 - FPR 阳性预测值 (PPV)PPV = TP / (TP + FP) 阴性预测值 (NPV)NPV = TN / (TN + FN) 假发现率 (FDR)FDR = FP / (FP + TP) Matthews相关系数 (MCC),即 Phi相关系数F1 = 2TP/(P+P') |
| Source: Fawcett (2006). |
ROC曲线
ROC空间将伪阳性率(FPR)定义为 X 轴,真阳性率(TPR)定义为 Y 轴。
TPR:在所有实际为阳性的样本中,被正确地判断为阳性之比率。
FPR:在所有实际为阴性的样本中,被错误地判断为阳性之比率。
给定一个二元分类模型和它的阈值,就能从所有样本的(阳性/阴性)真实值和预测值计算出一个 (X=FPR, Y=TPR) 座标点。
从 (0, 0) 到 (1,1) 的对角线将ROC空间划分为左上/右下两个区域,在这条线的以上的点代表了一个好的分类结果(胜过随机分类),而在这条线以下的点代表了差的分类结果(劣于随机分类)。
完美的预测是一个在左上角的点,在ROC空间座标 (0,1)点,X=0 代表着没有伪阳性,Y=1 代表着没有伪阴性(所有的阳性都是真阳性);也就是说,不管分类器输出结果是阳性或阴性,都是100%正确。一个随机的预测会得到位于从 (0, 0) 到 (1, 1) 对角线(也叫无识别率线)上的一个点;最直观的随机预测的例子就是抛硬币。
让我们来看在实际有100个阳性和100个阴性的案例时,四种预测方法(可能是四种分类器,或是同一分类器的四种阈值设定)的结果差异:
| A | B | C | C' | ||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
||||||||||||||||||||||||||||||||||||
| TPR = 0.63 | TPR = 0.77 | TPR = 0.24 | TPR = 0.76 | ||||||||||||||||||||||||||||||||||||
| FPR = 0.28 | FPR = 0.77 | FPR = 0.88 | FPR = 0.12 | ||||||||||||||||||||||||||||||||||||
| ACC = 0.68 | ACC = 0.50 | ACC = 0.18 | ACC = 0.82 |
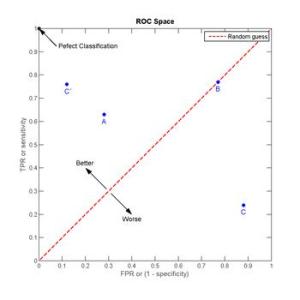 ROC空间的4个例子
ROC空间的4个例子
将这4种结果画在ROC空间里:
点与随机猜测线的距离,是预测力的指标:离左上角越近的点预测(诊断)准确率越高。离右下角越近的点,预测越不准。
在A、B、C三者当中,最好的结果是A方法。
B方法的结果位于随机猜测线(对角线)上,在例子中我们可以看到B的准确度(ACC,定义见前面表格)是50%。
C虽然预测准确度最差,甚至劣于随机分类,也就是低于0.5(低于对角线)。然而,当将C以 (0.5, 0.5) 为中点作一个镜像后,C'的结果甚至要比A还要好。这个作镜像的方法,简单说,不管C(或任何ROC点低于对角线的情况)预测了什么,就做相反的结论。
曲线下面积(AUC)
| A | B | C | C' | ||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
||||||||||||||||||||||||||||||||||||
| TPR = 0.63 | TPR = 0.77 | TPR = 0.24 | TPR = 0.76 | ||||||||||||||||||||||||||||||||||||
| FPR = 0.28 | FPR = 0.77 | FPR = 0.88 | FPR = 0.12 | ||||||||||||||||||||||||||||||||||||
| ACC = 0.68 | ACC = 0.50 | ACC = 0.18 | ACC = 0.82 |
 ROC空间的4个例子
ROC空间的4个例子
将这4种结果画在ROC空间里:
点与随机猜测线的距离,是预测力的指标:离左上角越近的点预测(诊断)准确率越高。离右下角越近的点,预测越不准。
在A、B、C三者当中,最好的结果是A方法。
B方法的结果位于随机猜测线(对角线)上,在例子中我们可以看到B的准确度(ACC,定义见前面表格)是50%。
C虽然预测准确度最差,甚至劣于随机分类,也就是低于0.5(低于对角线)。然而,当将C以 (0.5, 0.5) 为中点作一个镜像后,C'的结果甚至要比A还要好。这个作镜像的方法,简单说,不管C(或任何ROC点低于对角线的情况)预测了什么,就做相反的结论。
意义
| TP=77 | FP=77 | 154 |
| FN=23 | TN=23 | 46 |
| 100 | 100 | 200 |
计算
| TP=24 | FP=88 | 112 |
| FN=76 | TN=12 | 88 |
| 100 | 100 | 200 |
潜在问题
| TP=76 | FP=12 | 88 |
| FN=24 | TN=88 | 112 |
| 100 | 100 | 200 |
分析软件
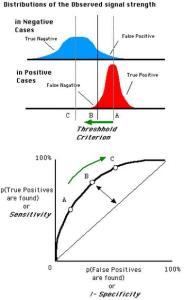 随着阈值调整,ROC座标系里的点如何移动
随着阈值调整,ROC座标系里的点如何移动
上述ROC空间里的单点,是给定分类模型且给定阈值后得出的。但同一个二元分类模型的阈值可能设定为高或低,每种阈值的设定会得出不同的FPR和TPR。
将同一模型每个阈值 的 (FPR, TPR) 座标都画在ROC空间里,就成为特定模型的ROC曲线。
例如右图,人体的血液蛋白浓度是呈正态分布的连续变数,病人的分布是红色,平均值为A g/dL,健康人的分布是蓝色,平均值是C g/dL。健康检查会测量血液样本中的某种蛋白质浓度,达到某个值(阈值,threshold)以上诊断为有疾病征兆。研究者可以调整阈值的高低(将左上图的B垂直线往左或右移动),便会得出不同的伪阳性率与真阳性率,总之即得出不同的预测准确率。
1. 由于每个不同的分类器(诊断工具、侦测工具)有各自的测量标准和测量值的单位(标示为:“健康人-病人分布图”的横轴),所以不同分类器的“健康人-病人分布图”都长得不一样。
2. 比较不同分类器时,ROC曲线的实际形状,便视两个实际分布的重叠范围而定,没有规律可循。
3. 但在同一个分类器之内,阈值的不同设定对ROC曲线的影响,仍有一些规律可循:
当阈值设定为最高时,亦即所有样本都被预测为阴性,没有样本被预测为阳性,此时在伪阳性率 FPR = FP / ( FP + TN ) 算式中的 FP = 0,所以 FPR = 0%。同时在真阳性率(TPR)算式中, TPR = TP / ( TP + FN ) 算式中的 TP = 0,所以 TPR = 0%
→ 当阈值设定为最高时,必得出ROC座标系左下角的点 (0, 0)。
当阈值设定为最低时,亦即所有样本都被预测为阳性,没有样本被预测为阴性,此时在伪阳性率FPR = FP / ( FP + TN ) 算式中的 TN = 0,所以 FPR = 100%。同时在真阳性率 TPR = TP / ( TP + FN ) 算式中的 FN = 0,所以 TPR=100%
→ 当阈值设定为最低时,必得出ROC座标系右上角的点 (1, 1)。
因为TP、FP、TN、FN都是累积次数,TN和FN随着阈值调低而减少(或持平),TP和FP随着阈值调低而增加(或持平),所以FPR和TPR皆必随着阈值调低而增加(或持平)。
→ 随着阈值调低,ROC点 往右上(或右/或上)移动,或不动;但绝不会往左下(或左/或下)移动。

-
江铃福特轻客持续打造最优TCO 锐骐超值版PK江铃国产共轨
2025-11-03 07:49:32 查看详情 -
江铃福特轻客持续打造最优TCO 江铃E200N豪华型怎么样
2025-11-03 07:49:32 查看详情 -
PRO上市 售价9.48万
2025-11-03 07:49:32 查看详情 -
380TSI劲擎智联版四驱车型上市 成都车展:雪铁龙C
2025-11-03 07:49:32 查看详情 -
欧拉新款R1将于成都车展上市 全新宝马2系Coupe最新谍照
2025-11-03 07:49:32 查看详情 -
西安大众速腾现金优惠2.3万 成都沃尔沃XC90优惠三万元
2025-11-03 07:49:32 查看详情 -
实拍江铃福特Equator 创富之选
2025-11-03 07:49:32 查看详情 -
实拍江铃福特Equator 江铃福特领界上市怎么选
2025-11-03 07:49:32 查看详情 -
Pro将于4月15日上市 12.9万元
2025-11-03 07:49:32 查看详情 -
捷途X95热爱Pro版上市 别克微蓝6插混车型上市
2025-11-03 07:49:32 查看详情


 求购
求购

