- 振荡周期

振荡周期
基本概念
振荡是指物理量或物理现象具有周期性往复变化的特性;振荡周期指物理量或物理现象完成一次振动所需时间,物理学上常用来描述电量的振荡周期。
通常情况下,振荡周期由波形图上两个相邻同方向峰值之间的时间间隔得到,与之相对应的物理量是振荡频率fp(频率),振荡频率和振荡周期互为倒数关系,即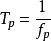 。
。
相关领域
电路电子学
振荡周期指电路中的电量(电流、电压等)在极大值和极小值之间随时间作周期性重复变化的时间间隔[2]。根据振荡的幅值变化分为等幅振荡、减幅振荡(衰减震荡)和增幅振荡(发散振荡),其波形图示意如概述插图所示。(推荐书籍:稻叶保著,《振荡电路的设计与应用》,科学出版社)
信号处理
振荡周期指周期性信号作周期性重复变化的时间间隔[3]。在信号处理领域,振荡周期即指周期信号的周期,因为对周期信号的处理是最基础和广泛的,不论是模拟信号还是数字信号,一种常用的处理方法就是将一个待处理信号延拓为周期信号进行处理[4]。
控制理论
在自动控制原理中,振荡周期指系统发生振荡时,输出作周期性重复变化的时间间隔。振荡周期属于系统评价的动态性能指标,可以用来衡量系统的动态性能。[5]
典型应用
简述
无论是在哪个专业领域中,振荡周期都有着相近的意义,即周期性变化的度量。任何发生振荡的系统都存在振荡周期的概念,无论是收敛(减幅)的还是发散(增幅)的。振荡周期或振荡频率都可以用来描述一个系统(包括电路)的动态性能。通常来说,振荡周期越小,系统的精度将会越高,这和我们日常生活中所听到的处理器(如电脑处理器)频率越高,一般性能越好是相对应的。
系统分析
在控制理论中,振荡是设计或分析控制系统所难以避免的问题,就设计来说,为了设计出一个符合要求的稳定系统,对振荡现象的控制是十分重要的。[5]
对典型二阶系统,自然频率(无阻尼振荡频率)![]() 和阻尼比ζ 对系统的响应情况起着决定作用。已知这两个参数则可以反映系统的具体振荡状态。
和阻尼比ζ 对系统的响应情况起着决定作用。已知这两个参数则可以反映系统的具体振荡状态。
ζ<0 时,系统不稳定,即发散,通常不讨论不稳定系统的振荡周期;
ζ=0 时,系统无阻尼(临界稳定),幅值不变;
0<ζ<1 时,系统为欠阻尼,会产生衰减振荡,通常研究的为欠阻尼情况;
ζ=1 时,系统为临界阻尼,不产生振荡;
ζ>1 时,系统为过阻尼,不产生振荡。
根据自然频率和阻尼比,可以得到更直观的系统时域动态性能指标参数,以二阶欠阻尼系统为例:
上升时间: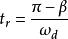 ,其中
,其中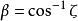 ,
, ,下同;
,下同;
峰值时间: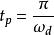 ;
;
超调量: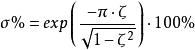 ;
;
另外还有调节时间、延迟时间、振荡次数等可参考胡寿松主编的《自动控制原理(第六版)》,P75-P78[5]
单片机/晶振
在单片机系统中,定时器/计数器的工作中,定时器需要借助单片机内部提供的脉冲进行定时,此时,定时的依据是CPU提供的周期性振荡,这个内部振荡的最大频率称为单片机的振荡频率,振荡一次所需的时间称为振荡周期,通常来说12个振荡周期成为一个机器周期,也就是进行一次运算/计数所需要的时间。此外,单片机系统也可以通过外部晶振提供振荡进行工作。

-
奥迪a4L保养周期及内容是什么
2025-11-01 09:37:43 查看详情 -
奥迪a4保养周期介绍【图】
2025-11-01 09:37:43 查看详情 -
电力系统低频功率振荡阻尼转矩分析理论与方法
2025-11-01 09:37:43 查看详情 -
96孔板微孔加热振荡器
2025-11-01 09:37:43 查看详情 -
汽车价格有哪些变化 为什么汽车价格会有周期性的上涨和下跌?
2025-11-01 09:37:43 查看详情


 求购
求购





