- lipschitz条件
- 首页
-
- 百科
-
- 发动机系统
-
- lipschitz条件
lipschitz条件
定义
![]() 对于在实数集的子集的函数
对于在实数集的子集的函数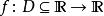 ,若存在常数,使得
,若存在常数,使得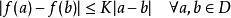 ,则称
,则称![]() 符合利普希茨条件,对于
符合利普希茨条件,对于![]() 最小的常数
最小的常数![]() 称为
称为![]() 的利普希茨常数。若
的利普希茨常数。若![]() ,
,![]() 称为收缩映射。
称为收缩映射。
利普希茨条件也可对任意度量空间的函数定义:
给定两个度量空间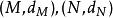 ,
,![]() 。若对于函数
。若对于函数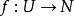 ,存在常数
,存在常数![]() 使得
使得
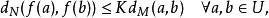 则说它符合利普希茨条件。
则说它符合利普希茨条件。
若存在![]() 使得
使得
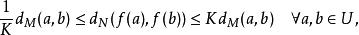 则称
则称![]() 为双李普希茨(bi-Lipschitz)的。[1]
为双李普希茨(bi-Lipschitz)的。[1]
皮卡-林德洛夫定理
若已知![]() 有界,
有界,![]() 符合利普希茨条件,则微分方程初值问题
符合利普希茨条件,则微分方程初值问题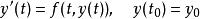 刚好有一个解。
刚好有一个解。
在应用上,![]() 通常属于一有界闭区间(如
通常属于一有界闭区间(如![]() )。于是
)。于是![]() 必有界,故
必有界,故![]() 有唯一解。
有唯一解。
例子
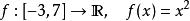 符合利普希茨条件,
符合利普希茨条件,![]() 。
。
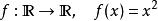 不符合利普希茨条件,当
不符合利普希茨条件,当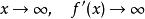 。
。
定义在所有实数值的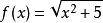 符合利普希茨条件,
符合利普希茨条件,![]() 。
。
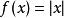 符合利普希茨条件,
符合利普希茨条件,![]() 。由此可见符合利普希茨条件的函数未必可微。
。由此可见符合利普希茨条件的函数未必可微。
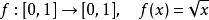 不符合利普希茨条件,
不符合利普希茨条件,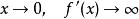 。不过,它符合赫尔德条件。
。不过,它符合赫尔德条件。
当且仅当处处可微函数f的一次导函数有界,f符利普希茨条件。这是中值定理的结果。所有![]() 函数都是局部利普希茨的,因为局部紧致空间的连续函数必定有界。[2]
函数都是局部利普希茨的,因为局部紧致空间的连续函数必定有界。[2]
性质
符合利普希茨条件的函数一致连续,也连续。
bi-Lipschitz函数是单射的。
Rademacher定理:若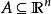 且
且![]() 为开集,
为开集,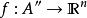 符利普希茨条件,则f几乎处处可微。
符利普希茨条件,则f几乎处处可微。
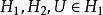 Kirszbraun定理:给定两个希尔伯特空间,
Kirszbraun定理:给定两个希尔伯特空间,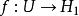 符合利普希茨条件,则存在符合利普希茨条件的
符合利普希茨条件,则存在符合利普希茨条件的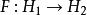 ,使得
,使得![]() 的利普希茨常数和
的利普希茨常数和![]() 的相同,且
的相同,且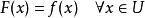 。[2]
。[2]

相关百科
-
380TSI劲擎智联版四驱车型上市 成都车展:雪铁龙C
2025-09-22 01:34:43 查看详情 -
Plus上市 别克昂科威S及昂科威S艾维亚将于7月29日上市
2025-09-22 01:34:43 查看详情 -
全新紧凑型SUV/上半年上市 别克昂科拉PLUS最新谍照
2025-09-22 01:34:43 查看详情 -
江铃福特轻客持续打造最优TCO 锐骐超值版PK江铃国产共轨
2025-09-22 01:34:43 查看详情 -
黄海纯电轿车Smile将于12月上市 29万元
2025-09-22 01:34:43 查看详情 -
江铃福特轻客持续打造最优TCO 江铃E200N豪华型怎么样
2025-09-22 01:34:43 查看详情 -
江铃宝典堪称商用皮卡常青树 江铃新宝典VS长城风骏7(图文)
2025-09-22 01:34:43 查看详情 -
Air正式上市 长安福特锐际将新增ST
2025-09-22 01:34:43 查看详情 -
西安大众速腾现金优惠2.3万 成都沃尔沃XC90优惠三万元
2025-09-22 01:34:43 查看详情 -
欧拉新款R1将于成都车展上市 全新宝马2系Coupe最新谍照
2025-09-22 01:34:43 查看详情


 求购
求购

