理想气体常数

气体常数表征理想气体热力学特性的一个常数。 为理想气体的绝对压力p和比容v 的乘积与热力学温度T之比。常以 符号“R”表示，单位为“J/(kg·K)”。 气体常数在数值上即相当于质量 为1kg的理想气体在可逆定压加热过程中温度每升高1K时对外所作出的膨胀功。其值仅取决于气体的种类，与气体所处的热力状态无关。例如氧气的R总是等于 259.8J/ (kg·K)、氮气的R恒为 296.7J/(kg·K)等。在工程热力学等学科中，常根据通用气体常数除以千摩尔质量或按迈耶公式来计算确定各种理想气体的气体常数。

理想气体常数因为各种真实气体在压力趋近于零时都趋近于理想气体，所以由实验测出，当温度为273.15K时，每摩尔任一气体的值都是22.414L，因此，在法定计量单位中R=8.314J·mol-1·K-1。

其它表达式：，其中 p 是气体压力，V是容积， m是气体质量， Rg某一种气体的气体常数， T 气体温度， R气体常数， M 气体的分子质量， n摩尔数。

R同时也出现在能斯特方程及洛伦兹-洛伦茨方程（Lorentz-Lorenz equation）中。

对于实际气体，R与压力、温度、气体种类有关。当温度较高、压力较低时，R近于常数。当T 较高，p→0时，无论何种气体，均有：

R=8.314472m3·MPa·mol-1·K-1

R=8.314472m3·Pa·mol-1·K-1

R=0.0820574587L·atm·mol-1·K-1(atm：一个标准大气压）

理想气体常数（或称摩尔气体常数、普适气体恒量）的数值随p和V的单位不同而异，以下是几种常见的表述：

在理想气体状态方程中，用于p、V和T刻画，表达这几个量之间的关系。

补充R单位推导：

由理想气体状态方程：pV=nRT 得：R=pv/（nT） [其中各个量的单位 p： pa， v：m3， n： mol， T： k]

带入单位进行推导：R[]=pa·m3/（mol·k）（其中pa·m3可以拆分为： pa·m2·m，而由F=PS知道 pa·m2即为N牛顿单位，由W=FS知道，N·m即为功的单位 J）所以通过以上代换可以得到R的单位：J/（mol·k）

1976年美国标准大气局将气体常数R *定义为：

R * = 8.31432×103N m kmol-1K-1。

注意使用千摩尔单位，导致常数中的因子为1000。 USSA1976承认该值与Avogadro常数和Boltzmann常数的引用值不一致。这种差异与准确性并不是显着的偏离，USSA1976将这个R *值用于标准气氛的所有计算。 当使用R的ISO值时，计算出的压力在11公里（相当于只有17.4厘米或6.8英寸的差异）上增加了0.62帕斯卡，而在20公里增加了0.292帕（相当于只有差异 0.338米或13.2英寸）。

任何情况 下绝对遵守玻意耳一马略特定律 、盖一吕萨克定律和查理定律的气体为理想气体。理想气体状态方程为pV=nRT，任何气体的摩尔数n=m（物质质量）/M（摩尔质量），则常数，求出p、V、m、M、T五个未知量，即可求出R。

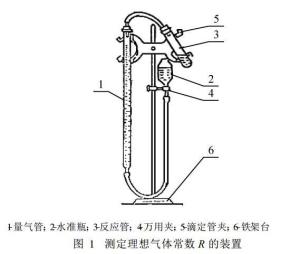
实验中先将 HCl用漏斗加入试管底部， 称取质量为mMg的 Mg 条一根，将Mg 条蘸少许水贴在反应试管内壁上 （尚未产生氢气 )，检验装置是否漏气 。证实其不漏气后，把水准瓶与量气管并列，使两者水面相平，然后记下量气管中水面读数 V初， 轻轻摇动试管， 使镁条落入酸中，反应产生的氢气使量气管中的水面下降，反应停止后，待试管冷却到室温，再次把水准瓶与量气管并列，使两者水面相平，记下量气管中水面读数 V终， 待整个体系的温度与室温相等后 ，用温度计测得室温 T，记录该温度下的大气压为 P0。^[1]则有：

式中△V = V终-V初，从 “分压定律“”的角度讨论得到的计算 R 的公式与已有化学实验教材中的公式是一致的。