- 十二边形

十二边形
多边形
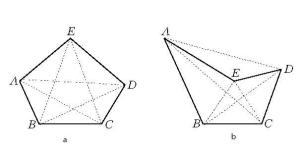 图1
图1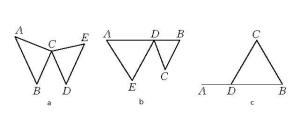 图2多边形,也称多角形,是平面几何中最基本、最重要的图形之一。广义地说,多边形就是封闭折线,但在平面几何中,采用以下稍窄的定义较为合适:平面上的多边形是由不自交的封闭折线和它所围成的区域共同组成的图形。这封闭折线所围成的区域称为多边形的内部,内部的点称为多边形的内点。平面的其他部分称为多边形的外部,外部的点称为多边形的外点。封闭折线的边称为多边形的边,折线的顶点称为多边形的顶点。顶点处两条边所夹的包含多边形内部的角称为多边形的角或内角。边数(即角数)是n的多边形称为n边形或n角形。连结多边形不相邻的两个顶点的线段称为多边形的对角线。多边形各边长度的和称为多边形的周长,这也就是封闭折线的长度。多边形常用连写它的各个顶点的字母来表示。如图1中a和b画的都是五边形ABCDE,它们的顶点是A,B,C,D,E,边是AB,BC,CD,DE,EA,对角线是AC,AD,BD,BE,CE,周长是五条边长度之和。
图2多边形,也称多角形,是平面几何中最基本、最重要的图形之一。广义地说,多边形就是封闭折线,但在平面几何中,采用以下稍窄的定义较为合适:平面上的多边形是由不自交的封闭折线和它所围成的区域共同组成的图形。这封闭折线所围成的区域称为多边形的内部,内部的点称为多边形的内点。平面的其他部分称为多边形的外部,外部的点称为多边形的外点。封闭折线的边称为多边形的边,折线的顶点称为多边形的顶点。顶点处两条边所夹的包含多边形内部的角称为多边形的角或内角。边数(即角数)是n的多边形称为n边形或n角形。连结多边形不相邻的两个顶点的线段称为多边形的对角线。多边形各边长度的和称为多边形的周长,这也就是封闭折线的长度。多边形常用连写它的各个顶点的字母来表示。如图1中a和b画的都是五边形ABCDE,它们的顶点是A,B,C,D,E,边是AB,BC,CD,DE,EA,对角线是AC,AD,BD,BE,CE,周长是五条边长度之和。
不自交的封闭折线可以出现两个顶点相重合,一个顶点在另一条边上及两条边有一部分(或全部)重合的特殊情形。因此,可以出现图2(a)的六边形ABCDEC、图2(b)的五边形和图2(c)的四边形。为排除以上情况,引进以下概念:由简单闭折线所围成的多边形称为简单多边形,其他多边形称为复杂多边形。上面图1是简单多边形,图2中都是复杂多边形。通常提到多边形都是指简单多边形[1]。
正十二边形
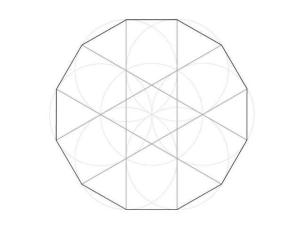 十二边形正十二边形,是指有十二条相等边的密封图形,每个内角均为150°。正十二边形跟等边三角形,或跟正方形、正六边形,可以密铺平面。正十二边形更是宇宙图形,接近圆,是很难画出的图形。三国时代数学家刘徽计算出半径为R的圆形,其内接正12边形的面积
十二边形正十二边形,是指有十二条相等边的密封图形,每个内角均为150°。正十二边形跟等边三角形,或跟正方形、正六边形,可以密铺平面。正十二边形更是宇宙图形,接近圆,是很难画出的图形。三国时代数学家刘徽计算出半径为R的圆形,其内接正12边形的面积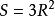 。
。
正十二边形的画法如图3所示,用圆规画圆,再画两条直径(要求垂直),交圆于点A、B、C、D。任意取一点A,r为半径作弧,交圆E,F两点。再取B~~,以此类推,最后再把这些交点连接起来,则是正十二边形 。
应用
(1)澳大利亚元的50分硬币形状为正12边形。澳门币五元和二毫的形状为正12边形,二毫和二元港币的形状为正12边形(严格地说,是每边向内凹陷的正十二边形)。
(2)嵩岳寺塔的底为正12边形。嵩山寺塔建于北魏正光四年(公元523年),是中国现存最早的砖塔,亦是楼阁式塔中最早的代表作。塔底层分二段:下段塔底平面为正十二边形,是中国佛塔仅见的平面形式(十二边形旨在象征佛教三世轮回教理的“十二因缘”说);上段为八角形。下段朴素无华,仅在四面砌门;上段八面各砌一单层方塔形壁龛,转角处砌壁柱,柱顶以宝珠、垂莲为饰,再上为叠涩砖砌,密檐15层。檐间部分很短,每面开一小窗,多数为假窗;第15层以上塔刹为石制,在覆莲上承受相轮与宝珠。全塔各层均向内收拢,外形呈曲线至塔顶,显得雄浑饱满,各檐叠涩轮廓为凹曲线,颇富韵味。塔外表原涂白灰,现大部分脱落,露出浅黄砖色。该塔全部用黄泥砌砖,历时千余年基本完好,说明当时我国高层建筑技术已达到相当高的水平。嵩山寺塔具有很高的历史价值和学术价值。

-
双十二魔券降临,江铃皮卡助力暖冬出行 实拍江铃新宝典(图文)
2025-09-21 15:07:46 查看详情 -
双十二魔券降临,江铃皮卡助力暖冬出行 9万元创富神车开回家
2025-09-21 15:07:46 查看详情 -
双十二魔券降临,江铃皮卡助力暖冬出行 低货台更轻松
2025-09-21 15:07:46 查看详情 -
中华人民共和国第十二届全国人民代表大会第三次会议
2025-09-21 15:07:46 查看详情 -
双十二魔券降临,江铃皮卡助力暖冬出行 首推尊领型
2025-09-21 15:07:46 查看详情


 求购
求购




