- 坐标变换公式

坐标变换公式
基本介绍
设V是域P上n维线性空间,且ε1,ε2,…,εn与ε′1,ε′2,…,ε′n皆是V的基,于是有:
ε′i=![]() ajiεj(i=1,2,…,n).
ajiεj(i=1,2,…,n).
以ε′i关于基ε1,ε2,…,εn的坐标(a1i,a2i,…,ani)为第i列构成的n阶矩阵(aij)称为由基ε1,ε2,…,εn到基ε′1,ε′2,…,ε′n的过渡矩阵,若α∈V关于基ε1,ε2,…,εn与基ε′1,ε′2,…,ε′n的坐标分别为(x1,x2,…,xn)与(x′1,x′2,…,x′n),则其两坐标间的关系,可由过渡矩阵(aij)表示为
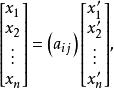 上式称为坐标变换公式[1]。
上式称为坐标变换公式[1]。
坐标变换公式的证明
设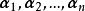 和
和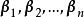 是线性空间Vn中的两个基,并且
是线性空间Vn中的两个基,并且
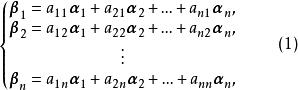 式(1)可表示为
式(1)可表示为
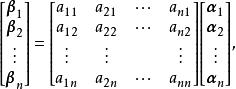 即
即
![]() 其中
其中
 ((2)式中A应为A的转置)式(1)或式(2)称为基变换公式,矩阵A称为由基
((2)式中A应为A的转置)式(1)或式(2)称为基变换公式,矩阵A称为由基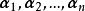 到基
到基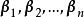 的过渡矩阵。
的过渡矩阵。
注意:式(1)中各式的系数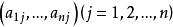 实际上是基向量
实际上是基向量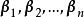 在基
在基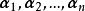 下的坐标[2]。
下的坐标[2]。
坐标变换公式及其证明:
定理1设Vn中一向量ξ在两个基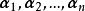 和
和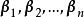 下的坐标分别是
下的坐标分别是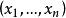 和
和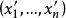 ,若两个基满足关系式(2) ,则有坐标变换公式:
,若两个基满足关系式(2) ,则有坐标变换公式:
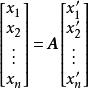 或
或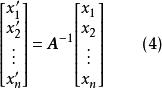
证明:因为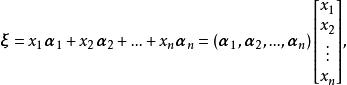
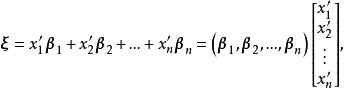
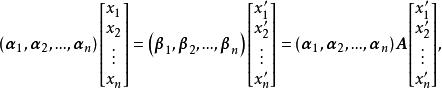 故由坐标的唯一性,得
故由坐标的唯一性,得
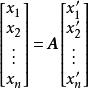 或
或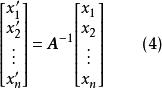
反之,设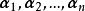 是线性空间Vn的一个基,A是n阶可逆矩阵,使得
是线性空间Vn的一个基,A是n阶可逆矩阵,使得
![]() 成立,可以证明:
成立,可以证明: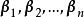 是Vn的n个线性无关的向量,从而也是Vn的一个基[2]。
是Vn的n个线性无关的向量,从而也是Vn的一个基[2]。
证明若数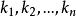 使
使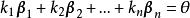 ,
,
即
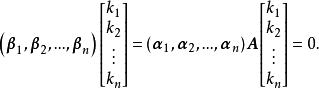 因为
因为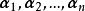 线性无关,故必有
线性无关,故必有
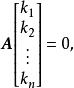 但A可逆,即|A|≠0,齐次线性方程组AX=0只有零解,必有
但A可逆,即|A|≠0,齐次线性方程组AX=0只有零解,必有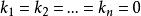 ,
,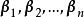 线性无关[2]。
线性无关[2]。

相关百科
-
MMF系列手动三坐标测量机
2025-11-03 17:23:39 查看详情 -
油耗怎么计算(油耗怎么计算公式多少钱一公里)
2025-11-03 17:23:39 查看详情 -
百公里油耗多少钱(百公里油耗多少钱怎么算公式)
2025-11-03 17:23:39 查看详情 -
怎么算油费(怎么算油费公式)
2025-11-03 17:23:39 查看详情 -
汽车油耗怎样计算(汽车油耗怎样计算公式)
2025-11-03 17:23:39 查看详情


 求购
求购





