埃尔米特多项式

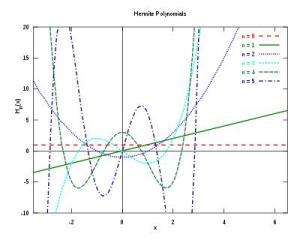前六个（概率论中的）埃尔米特多项式的图像。

埃尔米特多项式有两种常见定义。

第一种是概率论中较为常用的形式（又记作：）：

另一种是物理学中较为常用的形式（又记作：）：

这两种定义并不是完全等价的。它们之间的关系是：

概率论中常用第一种定义，因为是标准正态分布函数（数学期望等于0，标准差等于1）的概率密度函数。

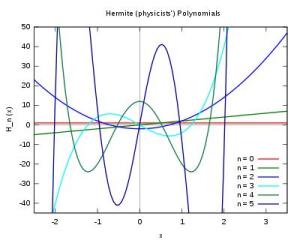前六个（物理学中的）埃尔米特多项式的图像。

前六个概率学和物理学中的埃尔米特多项式

序号	概率学	物理学

多项式H_n 是一个n次的多项式。概率论的埃尔米特多项式是首一多项式（最高次项系数等于1），而物理学的埃尔米特多项式的最高次项系数等于2ⁿ。

多项式H_n 的次数与序号n 相同，所以不同的埃尔米特多项式的次数不一样。对于给定的权函数 w，埃尔米特多项式的序列将会是正交序列。

   （概率论）

   （物理学）

也就是说，当m ≠ n 时：

除此之外，还有：

   （概率论）

   （物理学）

其中是克罗内克函数。

从上式可以看到，概率论中的埃尔米特多项式与标准正态分布正交。

在所有满足

的函数所构成的完备空间中，埃尔米特多项式序列构成一组基。其中的内积定义如下：