- 正定矩阵

正定矩阵
定义
正定矩阵
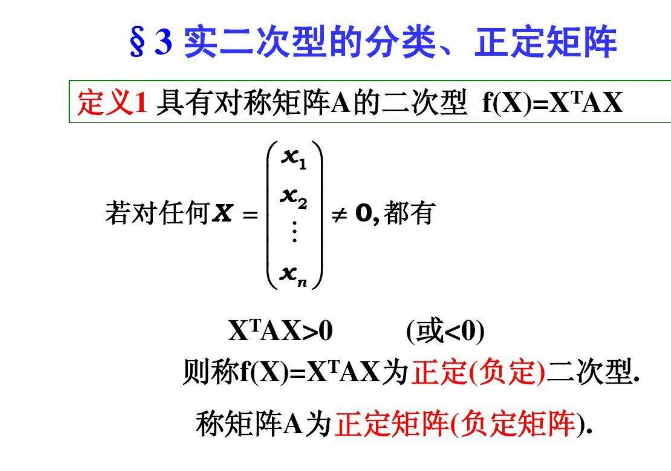 正定矩阵(4)(1)广义定义:设M是n阶方阵,如果对任何非零向量z,都有zTMz> 0,其中zT表示z的转置,就称M为正定矩阵。
正定矩阵(4)(1)广义定义:设M是n阶方阵,如果对任何非零向量z,都有zTMz> 0,其中zT表示z的转置,就称M为正定矩阵。
例如:B为n阶矩阵,E为单位矩阵,a为正实数。在a充分大时,aE+B为正定矩阵。(B必须为对称阵)
(2)狭义定义:一个n阶的实对称矩阵M是正定的的条件是当且仅当对于所有的非零实系数向量z,都有zTMz> 0。其中zT表示z的转置。
对称正定矩阵
设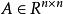 ,若
,若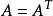 ,对任意的
,对任意的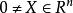 ,都有
,都有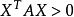 ,则称A为对称正定矩阵。
,则称A为对称正定矩阵。
Hermite正定矩阵
设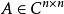 ,若
,若![]() ,对任意的
,对任意的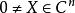 ,都有
,都有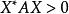 ,则称A为Hermite正定矩阵。
,则称A为Hermite正定矩阵。
性质
 正定矩阵(3)正定矩阵有以下性质:
正定矩阵(3)正定矩阵有以下性质:
(1)正定矩阵的行列式恒为正;
(2)实对称矩阵A正定当且仅当A与单位矩阵合同;
(3)若A是正定矩阵,则A的逆矩阵也是正定矩阵;
(4)两个正定矩阵的和是正定矩阵;
(5)正实数与正定矩阵的乘积是正定矩阵。
等价命题
对于n阶实对称矩阵A,下列条件是等价的:
(1)A是正定矩阵;
(2)A的一切顺序主子式均为正;
(3)A的一切主子式均为正;
(4)A的特征值均为正;
(5)存在实可逆矩阵C,使A=C′C;
(6)存在秩为n的m×n实矩阵B,使A=B′B;
(7)存在主对角线元素全为正的实三角矩阵R,使A=R′R。
充要条件
(1)n 元实二次型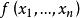 正定
正定![]() 它的正惯性指数为 n;
它的正惯性指数为 n;
(2) 一个实对称矩阵 A 正定![]() A 与 E 合同,即
A 与 E 合同,即![]() 可逆矩阵 C,使得
可逆矩阵 C,使得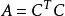 ;
;
(3) 实二次型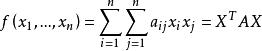 是正定的
是正定的![]() A的顺序主子式全大于零;
A的顺序主子式全大于零;
(4) 一个实对称矩阵 A 正定![]() A 的特征值全大于零;
A 的特征值全大于零;
(5) 一个实对称矩阵 A 正定![]() A 的主子式全大于零;
A 的主子式全大于零;
(6)A ,B 是实对称矩阵,则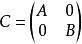 正定
正定![]() A,B均正定;
A,B均正定;
(7)A 实对称矩阵, A 正定![]()
![]() 正定矩阵 B,使得
正定矩阵 B,使得![]() ,(k 为任意正整数)。
,(k 为任意正整数)。
判定的方法
根据正定矩阵的定义及性质,判别对称矩阵A的正定性有两种方法:
(1)求出A的所有特征值。若A的特征值均为正数,则A是正定的;若A的特征值均为负数,则A为负定的。
(2)计算A的各阶主子式。若A的各阶主子式均大于零,则A是正定的;若A的各阶主子式中,奇数阶主子式为负,偶数阶为正,则A为负定的。
应用
对于具体的实对称矩阵,常用矩阵的各阶顺序主子式是否大于零来判断其正定性;对于抽象的矩阵,由给定矩阵的正定性,利用标准型,特征值及充分必要条件来证相关矩阵的正定性。

-
石家庄奥迪 石家庄裕华路联拓奥迪4S店离正定机场多少公里
2025-11-02 20:45:23 查看详情 -
河北正定师范高等专科学校
2025-11-02 20:45:23 查看详情


 求购
求购









