- 一致连续

一致连续
定义
设函数![]() 在区间I上有定义,如果对于
在区间I上有定义,如果对于![]() ,总有
,总有![]() ,使得对于在区间I上的任意两点
,使得对于在区间I上的任意两点![]() ,当
,当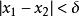 时,恒有
时,恒有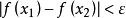 ,则称函数
,则称函数![]() 在区间I上一致连续。[1]
在区间I上一致连续。[1]
参数![]() 仅与
仅与![]() 有关,与所选取的任意两点
有关,与所选取的任意两点![]() 无关,即
无关,即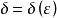 。
。
意义
从上述定义中可以看出,当函数在区间I上一致连续时,无论在区间I上的任何部分,只要自变量的两个数值接近到一定程度,总可以使相应的函数值达到预先指定的接近程度。[1]
定理
定理1Cantor定理或一致连续性定理
若函数![]() 在
在![]() 上连续,则
上连续,则![]() 在
在![]() 上一致连续。
上一致连续。
定理2
若函数![]() 为
为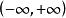 上的连续周期函数,则
上的连续周期函数,则![]() 在
在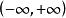 上一致连续。
上一致连续。
定理3
若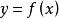 在有限开区间
在有限开区间![]() 上严格单调且连续,则其反函数
上严格单调且连续,则其反函数 在区间
在区间 上一致连续。
上一致连续。
定理4
设![]() 在
在![]() 上连续,若
上连续,若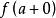 和
和![]() 都存在,则
都存在,则![]() 在
在![]() 上一致连续。
上一致连续。
定理5
设对于定义在区间I上的函数![]() ,
,![]() ,
,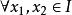 ,有
,有
![]()
成立,若![]() 在I上一致连续,则
在I上一致连续,则![]() 在I上也一致连续。[2]
在I上也一致连续。[2]
性质
1)设函数![]() 在区间
在区间![]() 和
和![]() 上一致连续,若
上一致连续,若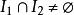 ,则
,则![]() 在
在![]() 上也一致连续;
上也一致连续;
2)若函数![]() 都在区间I上一致连续,则
都在区间I上一致连续,则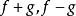 也在区间I上一致连续;
也在区间I上一致连续;
3)若![]() 在有限区间I上一致连续,则
在有限区间I上一致连续,则![]() 在I上有界;
在I上有界;
4)若函数![]() 都在有限区间I上的有界的一致连续函数,则
都在有限区间I上的有界的一致连续函数,则![]() 在区间I上也一致连续;
在区间I上也一致连续;
5)若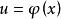 在定义域I上一致连续,其值域为U,
在定义域I上一致连续,其值域为U,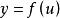 在U上一致连续,则
在U上一致连续,则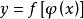 在I上一致连续。[2]
在I上一致连续。[2]
举例
函数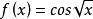 在
在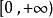 上一致连续。
上一致连续。
证明如下:
①任取![]() ,由三角函数可知
,由三角函数可知![]() 在闭区间
在闭区间![]() 上连续,由上述的定理1可知,
上连续,由上述的定理1可知,![]() 在
在![]() 上一致连续。
上一致连续。
②对于区间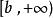 ,对
,对![]() ,取
,取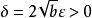 ,对
,对 ,当
,当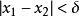 时,有
时,有
![]()
![]()
即![]() 在区间
在区间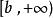 上一致连续。
上一致连续。
综上,![]() 在
在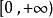 上一致连续。
上一致连续。

相关百科
-
长城炮打造全场景皮卡车生活 连续23年销冠是怎样炼成的
2025-09-21 23:57:44 查看详情 -
长城炮乘用皮卡全球版 连续23年销冠是怎样炼成的
2025-09-21 23:57:44 查看详情 -
长城造 连续23年销冠是怎样炼成的
2025-09-21 23:57:44 查看详情 -
长城炮带你开启浪漫之旅 连续23年销冠是怎样炼成的
2025-09-21 23:57:44 查看详情 -
听听长城风骏车主怎么说 连续23年销冠是怎样炼成的
2025-09-21 23:57:44 查看详情 -
长城炮带来野奢体验 连续23年销冠是怎样炼成的
2025-09-21 23:57:44 查看详情 -
长城炮带你清凉一夏 连续23年销冠是怎样炼成的
2025-09-21 23:57:44 查看详情 -
长城炮开启休旅新玩法 连续23年销冠是怎样炼成的
2025-09-21 23:57:44 查看详情


 求购
求购


