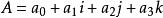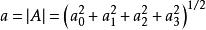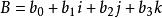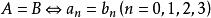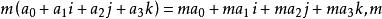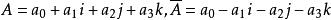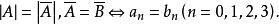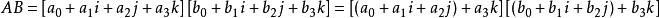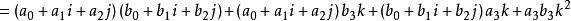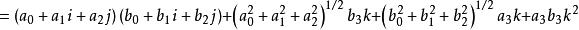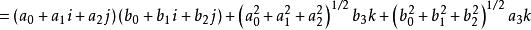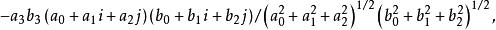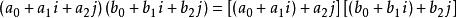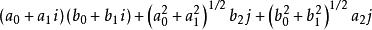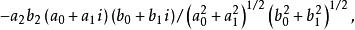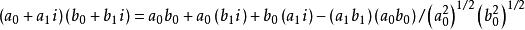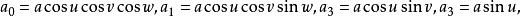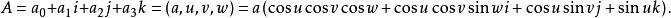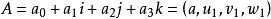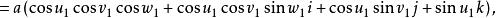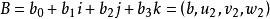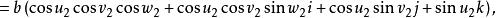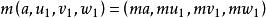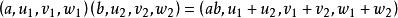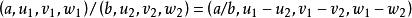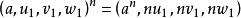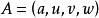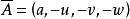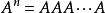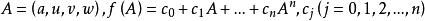- 超复数

超复数

相关百科
-
G10正式上市 续航或超350公里
2025-09-29 18:27:03 查看详情 -
东风雪铁龙C4L车内空气质量超豪车 对年轻的诠释
2025-09-29 18:27:03 查看详情 -
东风雪铁龙C4L车内空气质量超豪车 最新怎么样
2025-09-29 18:27:03 查看详情 -
东风雪铁龙C4L车内空气质量超豪车 欢迎品鉴
2025-09-29 18:27:03 查看详情 -
东风雪铁龙C4L车内空气质量超豪车 雪铁龙全新爱丽舍实拍图解
2025-09-29 18:27:03 查看详情 -
东风雪铁龙C4L车内空气质量超豪车 时尚前卫
2025-09-29 18:27:03 查看详情 -
东风雪铁龙C4L车内空气质量超豪车 店内有现车销售
2025-09-29 18:27:03 查看详情 -
东风雪铁龙C4L车内空气质量超豪车 试驾评测
2025-09-29 18:27:03 查看详情 -
东风雪铁龙C4L车内空气质量超豪车 款雪铁龙C5详细实拍
2025-09-29 18:27:03 查看详情 -
东风雪铁龙C4L车内空气质量超豪车 评测雪铁龙天逸C5
2025-09-29 18:27:03 查看详情


 求购
求购