RLC电路

图 1. RLC串联电路
V - 电源电压
I - 电路电流
R - 电阻
L - 电感
C - 电容
V - 电源电压
I - 电路电流
R - 电阻
L - 电感
C - 电容" bigsrc="https://pic.baike.soso.com/ugc/baikepic2/0/20180913191446-2046608455_png_180_249_4317.jpg/0" mark="" style="">

在此电路中，三个元件均与电压以串联方式连接。其主要的微分方程可将三个元件的本构方程代入基尔霍夫电压定律（KVL）获得。由基尔霍夫电压定律：

其中分别为R、L、C两端的电压，为随时间变化的电源的电压。将本构方程代入得到：

在电源电压为常数的情况下，对上式求导，并且除以L，得到以下二阶微分方程：

此方程可以写成更常用的形式：

称为“衰减量”，用于衡量当移除外部输入后，此电路的瞬态响应衰减的速率。为角共振频率。此二系数由下式给出：

，

阻尼系数是另一个常用的参数，定义为与的比值：

阻尼系数也可以由R、L、C求得：

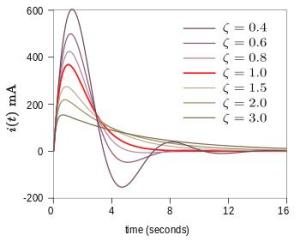
根据不同的阻尼系数的值，该微分方程的解法有三种不同的情况，分别为：欠阻尼（），过阻尼（），以及临界阻尼（）。该微分方程的特征方程为：

该方程的根为：

该微分方程的通解为两根指数函数的线性叠加：

系数A1以及 A2由具体问题的边界条件给出。

过阻尼响应

过阻尼响应（）为：

过阻尼响应是一个瞬态电流无振荡的衰减。

欠阻尼响应

欠阻尼响应（）为：

通过三角恒等式，这两个三角函数可用一个有相位的正弦函数表达：

欠阻尼响应是一个频率为的衰减的振荡。振荡衰减的速率为。指数里的描述了振荡的包络函数。B1 以及B2 （或第二种形式中的 B3 以及相位差 ）为任意常数，由边界条件确定。频率由下式给出：

这就是所谓的阻尼共振频率或阻尼固有频率。它是电路在无外部源驱动时自然振动的频率。谐振频率是电路在有外部源驱动时的谐振频率，为了便于区分常称作无阻尼谐振频率。

临界阻尼响应

临界阻尼响应（）为：

可以利用拉普拉斯变换分析RLC串联电路的交流暂态及稳态行为。若上述电压源产生的波形，在拉普拉斯变换后为V(s)（其中s为复频率），则在拉普拉斯域中应用基尔霍夫电压定律：

其中I(s)为拉普拉斯变换后的电流，求解I(s)：

在重新整理后，可以得到下式：

拉普拉斯导纳

求解拉普拉斯导纳Y(s)：

可以利用以上章节定义的参数α及ωo来简化上式，可得：

极点和零点

Y(s) 的零点是使得 的s：

    及    

Y(s) 的极点是使得 的s，求解二次方程，可得：

Y(s)的极点即为前文中提到微分方程之特征方程的根及。

正弦稳态

正弦稳态可通过令来表示，其中为虚数单位。

将此代入上面方程的幅值中：

以 ω 为变量的电流的函数为

有一个峰值。在此特殊情况下，这个峰值中的 ω 等于无阻尼固有谐振频率：

图 5. RLC 并联电路
V - 电源电压
I - 电路电流
R - 电阻
L - 电感
C - 电容" titlename="图 5. RLC 并联电路
V - 电源电压
I - 电路电流
R - 电阻
L - 电感
C - 电容

RLC并联电路的特性可以利用电路的对偶性，将RLC并联电路视为RLC串联电路的对偶阻抗来处理，就可以用类似RLC串联电路的分析方式来分析RLC并联电路。

RLC并联电路的衰减量可以用下式求得：

而其阻尼系数为：

若不考虑的系数，RLC并联电路的阻尼系数恰好是RLC串联电路阻尼系数的倒数。

频域

图 6. 正弦稳态分析以R = 1 欧姆、C = 1 法拉、L = 1 亨利、V = 1.0 伏特来进行正规化" titlename="图 6. 正弦稳态分析以R = 1 欧姆、C = 1 法拉、L = 1 亨利、V = 1.0 

将并联各元件的导纳相加，即为此电路的导纳：

电容、电阻及电感并联后，在共振频率的阻抗为最大值，和电容、电阻及电感串联的情形恰好相反，RLC并联电路是抗共振电路（antiresonator）。

右图中可以看出若用定电压驱动时，电流的频率响应在共振频率处有最小值。若用定电流驱动，电压的频率响应在共振频率处有最大值，和RLC串联电路中，电流的频率响应图形类似。

 RLC并联电路，电阻和电感串联" 所示，电阻与电感串联的并联LC电路是有必要考虑到线圈卷线的电阻时经常遇到的一种拓扑结构。并联LC电路经常用于带通滤波中，而 Q 因子主要由此电阻决定。电路的谐振频率为，

这是电路的谐振频率，定义为导纳虚部为零时的频率。在特征方程的一般形式（此电路与之前的相同）中出现的频率

不是相同的频率。在这种情况下是固有的无阻尼谐振频率

阻抗幅值最大时的频率为，

其中是线圈的品质因数。这可以下式很好地近似

此外，精确的最大阻抗幅值由下式给出，

.

值比1大时，可以用下式很好地近似

.

同样，电阻与电容并联的串联LC电路可用于有耗介质的电容器。这种构造如图8所示。在这种情况下谐振频率（阻抗的虚部为零时的频率），由下式给出，

而阻抗幅值最大时的频率为

其中