- 正弦曲线

正弦曲线
定义
正弦曲线可表示为y=Asin(ωx+φ)+k,定义为函数y=Asin(ωx+φ)+k在直角坐标系上的图象,其中sin为正弦符号,x是直角坐标系x轴上的数值,y是在同一直角坐标系上函数对应的y值,k、ω和φ是常数(k、ω、φ∈R且ω≠0)
A——振幅,当物体作轨迹符合正弦曲线的直线往复运动时,其值为行程的1/2。
(ωx+φ)——相位,反映变量y所处的状态。
φ——初相,x=0时的相位;反映在坐标系上则为图像的左右移动。
k——偏距,反映在坐标系上则为图像的上移或下移。
ω——角速度, 控制正弦周期(单位弧度内震动的次数)。
一般形式
正弦曲线的形状就像完美的海上波浪般,以三角函数正弦比例改变而形成。[1]
标准的纯正弦函数公式为
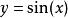 sin(x) 为正弦函数。
sin(x) 为正弦函数。
而一般应用的正弦曲线公式为
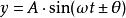 A 为波幅(纵轴), ω 为角频率, t 为时间(横轴), θ 为相偏移(横轴左右)。
A 为波幅(纵轴), ω 为角频率, t 为时间(横轴), θ 为相偏移(横轴左右)。
以下的公式则拥有全部的可用参数
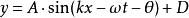 k 为波数(周期密度), D 为(直流)偏移量(y轴高低)。
k 为波数(周期密度), D 为(直流)偏移量(y轴高低)。
性质
(1)正弦函数是一条波浪线,当x∈R时定与x轴相交但不一定过(0,0)。
(2)在波形移动的时候需要注意的是:振幅A变大,波形在y轴上最大与最小值的差值变大;振幅A变小,则相反;角速度ω变大,则波形在X轴上收缩(波形变紧密);角速度ω变小,则波形在X轴上延展(波形变稀疏)。
(3)另外一点就是如果给出的是y=Asin(ωx+φ),则想移动波形向左或者向右,那么应该是先化为这个形式的式子y=Asin[ω(x+φ/ω)],如果想向右移动m弧度,就变为y=Asin[ω(x+φ/ω-m)],反之,向左移动的话变为y=Asin[ω(x+φ/ω+m)],记住在给自变量加或者是减m才达到移动波形的目的。
产生
正弦曲线的出现和应用非常广泛,可经常见于研究和使用于:[2]
- 信号处理的模拟信号
- 物理的简谐运动
- 声学的声音空气振动
- 乐器音叉的振动波
- 频率产生器的输出
- 交流电的电压改变
等等。
即使是其它不规则的非正弦波,其实亦能够以不同周期和波幅的正弦波集合来表示。这类将复杂波段化成正弦波的技术称为傅立叶分析。



 求购
求购








