- 可行域

可行域
基本介绍
所谓约束集合,就是指所有不等式约束和等式约束的交集。在此集合内所有设计点x都满足全部的约束条件,故又称它为设计可行域,表示为:
 其中假设函数
其中假设函数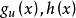 和h(x)都是连续的。这样,对于一个约束的优化设计问题,由于约束面的存在而把设计空间划分为两个区域:设计可行域D和非可行域。因而,最优解或可接受设计解只能从可行域内的各点中产生。
和h(x)都是连续的。这样,对于一个约束的优化设计问题,由于约束面的存在而把设计空间划分为两个区域:设计可行域D和非可行域。因而,最优解或可接受设计解只能从可行域内的各点中产生。
显然,若在可行域内不存在设计点,则认为此可行集合是个空集,此时也就得不到一个设计解,问题就可能出于所建立的约束条件与设计要求是相矛盾的。
关于约束可行域D是否为一个凸集,在凸规划理论中证明了:若各个不等约束函数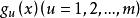 是凸函数和等式约束
是凸函数和等式约束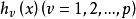 是线性函数,则D是凸集。但是只要等式约束是非线性的,那么集合D一定是个非凸集[2]。
是线性函数,则D是凸集。但是只要等式约束是非线性的,那么集合D一定是个非凸集[2]。
可行域的其他性质
【例1】对于一个二维问题,当其约束条件为:
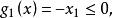
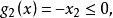
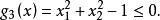
由图1 (a)可见,它是一个在第一象限内的凸集;当约束条件改为:
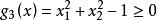 时,由图1 (b)可见,是一个在第一象限内的非凸集D,因为
时,由图1 (b)可见,是一个在第一象限内的非凸集D,因为![]() 函数是一凹函数;当约束条件
函数是一凹函数;当约束条件![]() 取为等式约束
取为等式约束
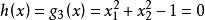 时,由图1 (c)可见,也是一个非凸集,此时这个集合是在x1≥0和x2≥0(第一象限内)上
时,由图1 (c)可见,也是一个非凸集,此时这个集合是在x1≥0和x2≥0(第一象限内)上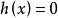 的一段曲线。
的一段曲线。
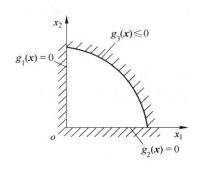 图1(a)凸集
图1(a)凸集
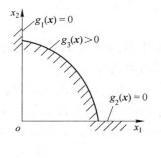 图1 (b)非凸集
图1 (b)非凸集
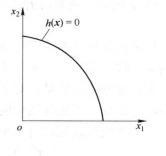 图1(c)非凸集
图1(c)非凸集
值得注意的是,一个约束函数经过变换,虽然表示形式不同但未改变其约束条件的性质,但有时却会影响约束函数的凸性,例如,对于x1>0和x2>0,且a和b为正常数,其原约束条件形式为:
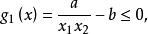 可以等价地变换为下面形式(由于x1和x2均取正值,故不等式的意义没有改变):
可以等价地变换为下面形式(由于x1和x2均取正值,故不等式的意义没有改变):
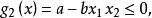 结果是
结果是![]() 是凸函数,变换为
是凸函数,变换为![]() 则是非凸函数,因为它们的Hessian矩阵分别为:
则是非凸函数,因为它们的Hessian矩阵分别为:
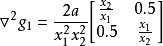 和
和
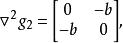 式中,
式中,![]() 为正定矩阵;
为正定矩阵;![]() 为不定矩阵。
为不定矩阵。
由此,约束函数通过形式上的变换,结果可能丢失了函数的凸性(或者相反),这也就影响可行域的约束集合的凸性条件。
根据上述可以推知,在n维欧氏空间Rn中,由一组不等式约束函数可以组成一个或几个可行域D。对于仅由一组等式约束所组成的可行域D,如果这组方程的函数是连续且彼此独立的,那么这个可行域D就是一个n-p维的子集。
对于由一组非线性约束函数所定义的可行域,确定它是凸集还是非凸集,一般说来是比较困难的,而且对于一个非凸的集合,往往是造成一个优化设计问题有多个约束极值的重要原因[2]。

-
实拍江铃域虎7钓鱼版 试驾江铃E400
2025-09-23 06:27:35 查看详情 -
江铃域虎7商乘全能铸就经典 实力超值
2025-09-23 06:27:35 查看详情 -
江铃域虎7商乘全能铸就经典 空间满足家用
2025-09-23 06:27:35 查看详情 -
和江铃域虎9来一场户外探索 多重补贴超值购
2025-09-23 06:27:35 查看详情 -
江铃域虎7商乘全能铸就经典 低货台更轻松
2025-09-23 06:27:35 查看详情 -
和江铃域虎9来一场户外探索 江铃宝典让你搬运更便捷
2025-09-23 06:27:35 查看详情 -
江铃域虎7商乘全能铸就经典 试驾评测
2025-09-23 06:27:35 查看详情 -
江铃宝典堪称商用皮卡常青树 和江铃域虎9来一场户外探索
2025-09-23 06:27:35 查看详情 -
和江铃域虎9来一场户外探索 江铃福特轻客持续打造最优TCO
2025-09-23 06:27:35 查看详情 -
和江铃域虎9来一场户外探索 实拍江铃新宝典(图文)
2025-09-23 06:27:35 查看详情


 求购
求购

