FP-growth

众所周知，Apriori算法在产生频繁模式完全集前需要对数据库进行多次扫描，同时产生大量的候选频繁集，这就使Apriori算法时间和空间复杂度较大。但是Apriori算法中有一个很重要的性质：频繁项集的所有非空子集都必须也是频繁的。但是Apriori算法在挖掘额长频繁模式的时候性能往往低下，Jiawei Han提出了FP-Growth算法。

FP-Tree：将事务数据表中的各个事务数据项按照支持度排序后，把每个事务中的数据项按降序依次插入到一棵以 NULL为根结点的树中，同时在每个结点处记录该结点出现的支持度。

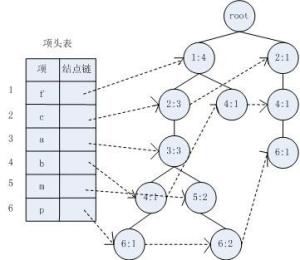FP-Tree结构图

条件模式基：包含FP-Tree中与后缀模式一起出现的前缀路径的集合

条件树：将条件模式基按照FP-Tree的构造原则形成的一个新的FP-Tree

基本思路：不断地迭代FP-tree的构造和投影过程

算法描述如下：

1、对于每个频繁项，构造它的条件投影数据库和投影FP-tree。

2、对每个新构建的FP-tree重复这个过程，直到构造的新FP-tree为空，或者只包含一条路径。

3、当构造的FP-tree为空时，其前缀即为频繁模式；当只包含一条路径时，通过枚举所有可能组合并与此树的前缀连接即可得到频繁模式。

构造FP-Tree

挖掘频繁模式前首先要构造FP-Tree，算法伪码如下：

输入:一个交易数据库DB和一个最小支持度threshold.

输出:它的FP-tree.

步骤:

1.扫描数据库DB一遍.得到频繁项的集合F和每个频繁项的支持度.把F按支持度递降排序,结果记为L.

2.创建FP-tree的根节点,记为T,并且标记为’null’.然后对DB中的每个事务Trans做如下的步骤.

根据L中的顺序,选出并排序Trans中的事务项.把Trans中排好序的事务项列表记为[p|P],其中p是第一个元素,P是列表的剩余部分.调用insert_tree([p|P],T).

函数insert_tree([p|P],T)的运行如下.

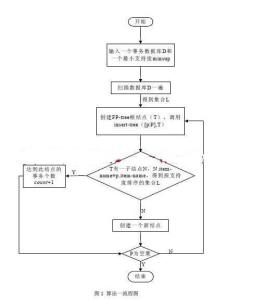FP-Tree创建的算法流程图如果T有一个子结点N,其中N.item-name=p.item-name,则将N的count域值增加1;否则,创建一个新节点N,使它的count为1,使它的父节点为T,并且使它的node_link和那些具有相同item_name域串起来.如果P非空,则递归调用insert_tree(P,N).

注：构造FP-Tree的算法理解上相对简单，所以不过多描述

挖掘频繁模式

对FP-Tree进行挖掘，算法如下：

输入:一棵用算法一建立的树Tree

输出:所有的频繁集

步骤:

调用FP-growth(Tree,null).

procedure FP-Growth ( Tree, x)

{

(1)if(Tree只包含单路径P)then

(2) 对路径P中节点的每个组合（记为B）

(3) 生成模式B并x，支持数=B中所有节点的最小支持度

(4) else 对Tree头上的每个ai，do

{

(5) 生成模式B= ai 并 x，支持度=ai.support；

(6) 构造B的条件模式库和B的条件FP树TreeB；

(7)ifTreeB !=空集

(8)thencall FP-Growth ( TreeB , B )

}

}

下图给出了整个算法的演示过程：

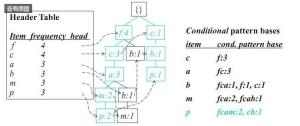FP-Growth算法实例演示图(3)