- 空间相干

空间相干
简介
空间相干是指光场中不同的空间同一时刻波场的相关性。杨氏实验装置是分析空间相干性的典型实例。
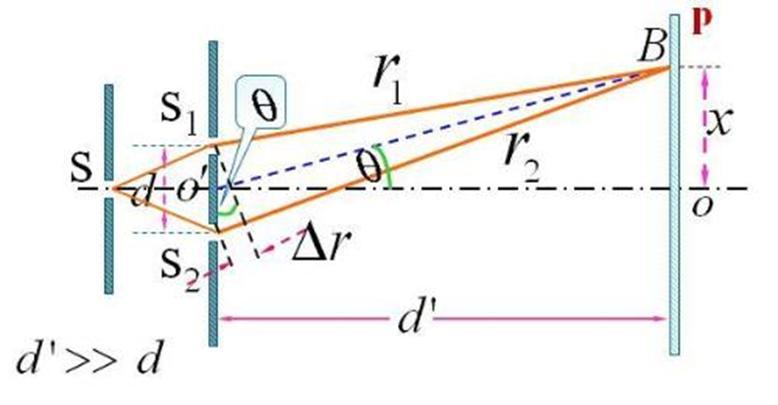
因此当OO'=∆X时是极限宽度(∆X 是条纹间距),由前面的公式可得:
![]()
上式中,b是极限宽度,D是相干间隔。
相干面积
在这截面上各点的光都是相干的。
光源的有效使用面积:是光源产生有效面积的允许尺寸。
因为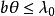 ,而
,而![]() 。所以
。所以
![]()
令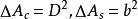 ,则有
,则有
![]()
光源尺寸对干涉效应的影响
由于空间相干性的要求而提出的对光源尺寸的要求是:因光源引起的附加光程差应小于λ/2。实际上,为使干涉条纹清晰,对光源的要求更加严格,光源引起的附加光程差应小于λ/4。
但是从使用的角度看,总希望光源尺寸大些,以使入射光强度大些,这样更有利于观察。
对于每种具体的干涉装置,都应根据被测预先估计所允许的光源大小。
例如:
(1) 双缝干涉,对光源的要求是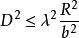 ,它限制了光源的有效使用面积。
,它限制了光源的有效使用面积。
(2) 等厚干涉,对光源的要求是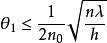 ,限制了光源的尺寸。
,限制了光源的尺寸。
注意:平行光入射的等厚干涉观察装置中,对光源的允许尺寸是:
![]()
等厚干涉
单色点光源引起的等厚干涉条纹:
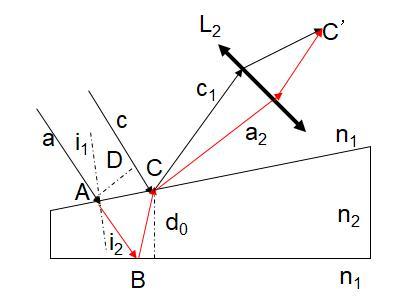
(1)装置:在一均匀透明介质n1中放入上下表面成一微小夹角 的均匀透明介质薄膜n2(也称劈尖) ,用单色点光源照射薄膜,其反射和透射光如图所示。
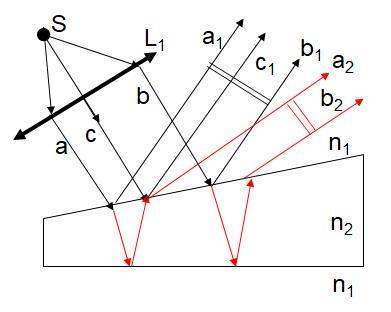
(2)光路分析:如图所示。C’可视为C的象。
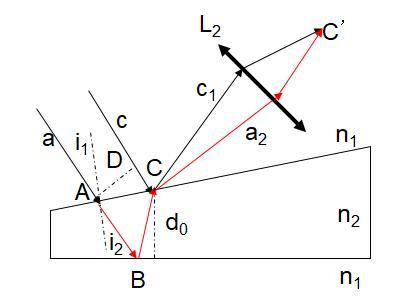
(3)相干性分析:
如上图所示,两光束c1和a2由同一光源发出且有几乎有相同的传播方向,所以频率相同、相差恒定、振动方向相同,是相干光束。
(4)光程差:如上图所示。
额外程差:
无论n1<n2还是n1>n2,在两反射光束中,始终存在半波损失,故有λ/2的额外程差
光程差:两光束的光程差为:
![]()
其中,额外程差取—λ/2
由于一般情况下薄膜很薄,且上、下两表面夹角很小,所以,推导得:
![]()
(5)干涉公式:
当下式成立时,
![]()
干涉相长,亮纹;
当下式成立时,
![]()
干涉相消,暗纹。
扩展光源
激光出现前,所有的光源(例如过去光学实验室中使用的白炽灯、钠灯、汞灯等)都可称为扩展光源。用激光照射散射物体形成的散射光束也是扩展光源。扩展光源的特点是发光面积较大,光线出射方向(波矢量)极多。或者说他的空间频谱极宽,相干面积极小。也就是空间相干性极差。
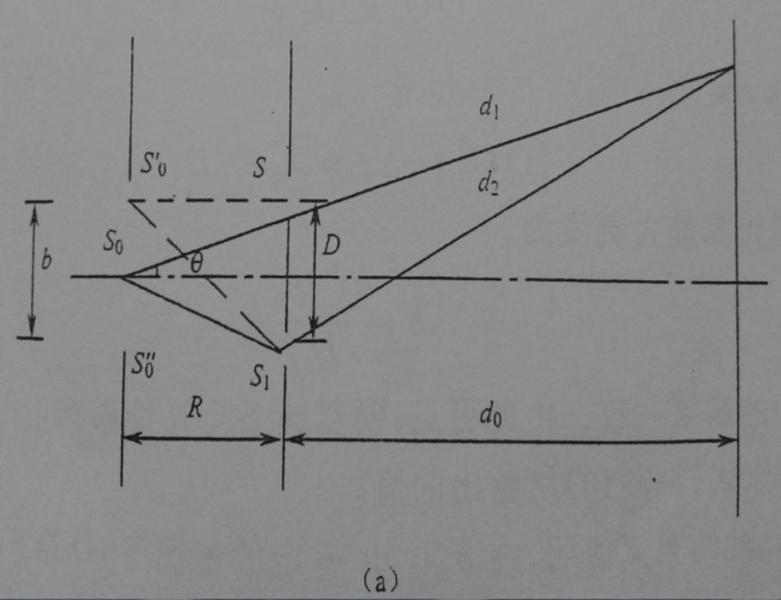
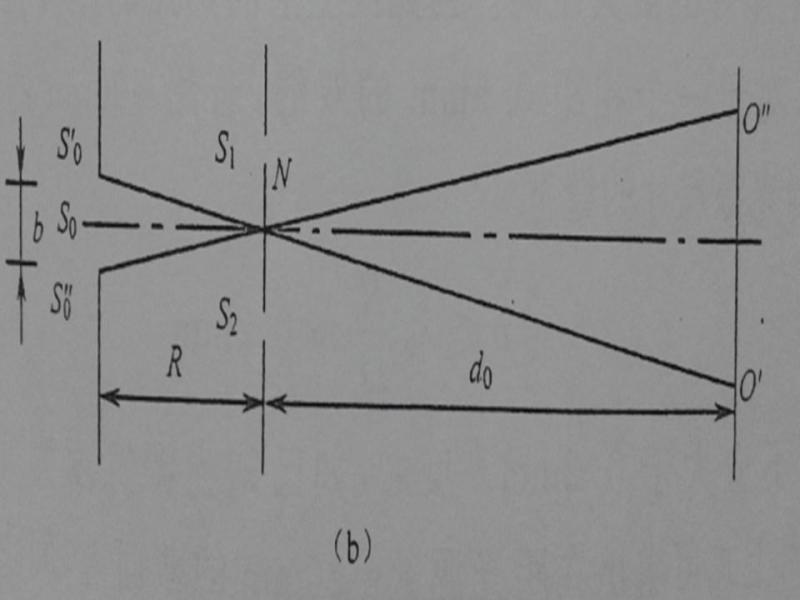
范西特-泽尼克定理
如下图所示,
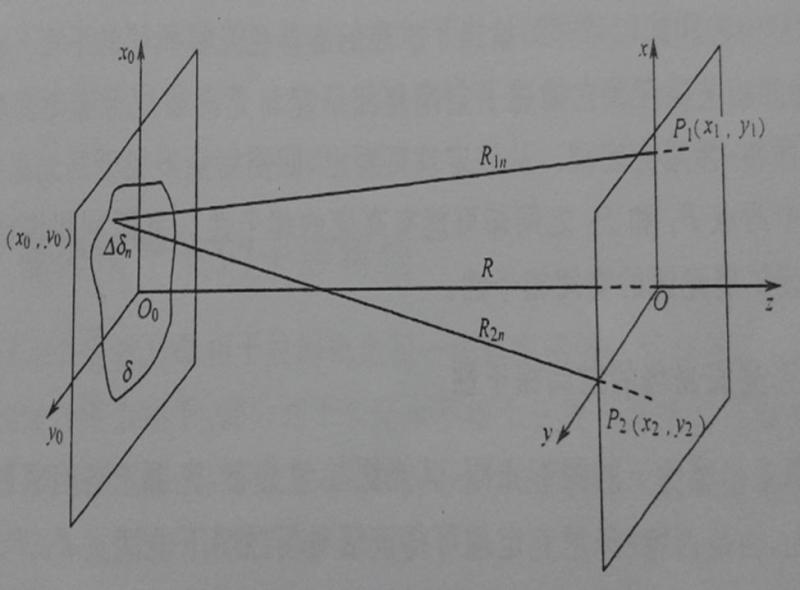
p1、 p2两点的总光强为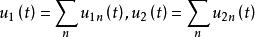 。
。
其中,
![]()
![]()
复相干因子为μ:
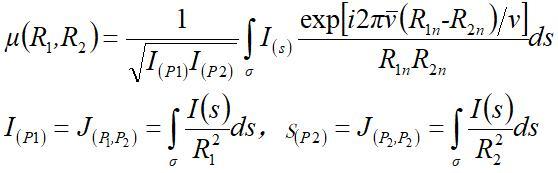
以上式子描述了空间复相干度与光源强度分布之间的关系。称之为范西特-泽尼克定理。
该定理可以看出,即使完全不相干的光源,经传播后其辐射场中p1、 p2 两点之间却可能有高度的相干性。其原因在于,虽然光源面上两点互不相关,但在观察点p1、 p2 处的光振动分别有来自光源上同一点振动的贡献。圆形光源和狭缝光源的空间相干性就是两个典型的例子。
部分相干光的干涉特性
实际的光源由于不仅有一定的限度,而且具有一定的谱宽,因而总是部分相干。
复相干度是:光源相干性的量度,表示相干部分所占总强度的比例。
观察部分相干光的干涉时,其条纹的对比度与光源尺度和频谱宽度有关。
(1)完全相干光:条纹对比度等于1;
(2)完全不相干光 :条纹对比度等于0;
(3)部分相干光:条纹对比度在0~1。
干涉条纹的定域性
定域就是某个一定的区域,非定域就是空间任何区域。
两个单色相干点源(双缝干涉)发出的光,总有一确定的光程差,从而产生一定的强度分布,并能观察到清晰的干涉条纹,这种干涉称为非定域干涉。就是在任何地方都能看到。
在扩展光源的情况下(一个光源,但是,不是点光源,可以看作是很多点光源的集合),由光源上不同的点出发的光线到达空间的该点,产生双光束干涉的两支相干光的光程差不同。在光程差变化大于四分之波长的区域观察不到干涉条纹,小于四分之波长的区域,尽管采用了扩展光源,仍可观察到清晰干涉条纹.可观察到清晰干涉条纹的区域称为定域区。
激光的相干性
光源的时间相干性体现为其单色性,即所发射光子频率的离散程度。其具体数值指标为谱线宽度,其值越小说明发射光子频率的离散程度越小,光源的单色性越好,其时间相干性越好。
(1)理想的激光是一个纯单色振荡,即只有一个频率的光能满足谐振条件,其产生的广场可表示为:
![]()
由于各种线宽加宽效应,使得单纵模激光具有一定的谱宽。(He-Ne激光器其谱宽约为106Hz)
(2)很多激光器都输出多纵模,其产生的场可表示为:
![]()
即使对多纵模的激光,其频谱任很窄。
普通单色光源的谱线宽度的数量级为千分之几纳米到几纳米,而激光的谱线宽度只有10-9nm甚至更小,因此,激光的时间相干性要远远优于普通单色光源。
光源的空间相干性体现为光源的大小对相干性的影响。由于从普通光源的不同部位发出的光是不相干,因此光源的大小必然影响到其相干性。
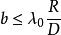 此来衡量光源的空间相干性。由于激光光源各处发出的光都是相干的,所以激光光源的光场减小了相干间隔的限制,这也是激光具有强相干性的原因之一。
此来衡量光源的空间相干性。由于激光光源各处发出的光都是相干的,所以激光光源的光场减小了相干间隔的限制,这也是激光具有强相干性的原因之一。
激光的空间相干性主要取决于其横模的结构,即输出光束在空间的分布。
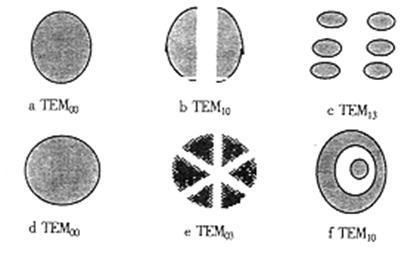
对于多横模结构的激光器,相当于多个光源的组合,其频率、偏振及位置各不相同,因而彼此不相干。但每个横模各自都分别是良好的相干光源,在其整个横截面内都是空间相干的。

-
实拍江铃新宝典(图文) 空间满足家用
2025-06-15 17:36:48 查看详情 -
江铃域虎7商乘全能铸就经典 空间满足家用
2025-06-15 17:36:48 查看详情 -
江铃福特轻客持续打造最优TCO 空间满足家用
2025-06-15 17:36:48 查看详情 -
航天恒星空间技术应用有限公司
2025-06-15 17:36:48 查看详情


 求购
求购




