- 六连环

六连环
基本介绍
若A,B,C,D为定圆上的四个点,分别通过A和B,B和C,C和D,D和A各作一圆轮回相交(如图所示),则所得另外四个交点A′,B′,C′,D′共圆或共线.当所得四交点共圆时,此图形共有六个圆,称此六个圆为六连环[2]。
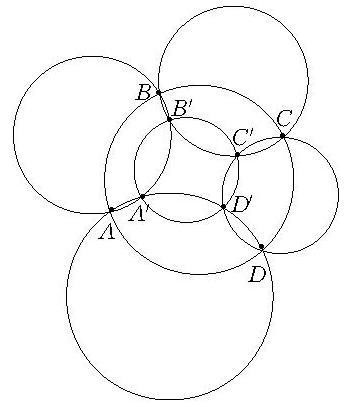 图1 六连环
图1 六连环
若将其中圆改为定直线,命题仍直确,即:
定理设定直线上有四点,通过其第一第二两点,第二第三两点,第三第四两点,第四第一两点,各作一圆轮回相交,则所得四个第二交点共圆(图2)或共线(图3)。
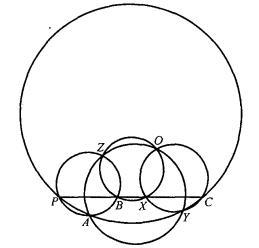 图2
图2
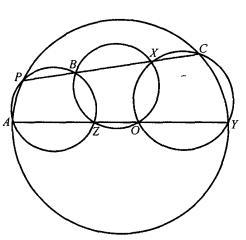 图3
图3
六连环定理的证明
证明六连环定理:四圆循环相交,如果其中有四个交点共圆或共线,则另外四个交点也共圆或共线。
证明如图4~7所示,设四个圆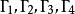 循环相交于点
循环相交于点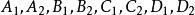 ,且A₁、B₁、C₁、D₁四点在圆(直线)
,且A₁、B₁、C₁、D₁四点在圆(直线)![]() 上。
上。
以D₁为反演中心任作一反演变换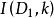 ,设点X的反点为X',则
,设点X的反点为X',则![]() 的反形分别为直线
的反形分别为直线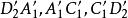 ,且
,且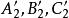 分别在直线
分别在直线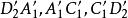 上,
上,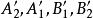 四点共圆,
四点共圆,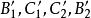 四点共圆(图7)。于是有
四点共圆(图7)。于是有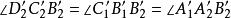 ,因此,
,因此,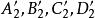 四点共圆,从而它们的反点
四点共圆,从而它们的反点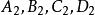 四点共圆或共线[3]。
四点共圆或共线[3]。
六连环定理证明Miquel定理
利用六连环定理极易证明下面的Miquel定理。
五角星的五边交成一个凸五边形和五个三角形,则五个三角形的五个外接圆的异于五边形的顶点的五个交点在一个圆上。
事实上,如图8所示,设五角星的五个顶点分别为H、K、L、M、N,它的五边交成凸五边形ABCDE和五个三角形:△AHB、△BKC、△CLD、△DME、△ENA,这五个三角形的五个外接圆异于A、B、C、D、E的五个交点为P、Q、R、S、T,易知,点P、S都在△HLE的外接圆上,在⊙(AHB)、⊙(BKC)、⊙(CLD)、⊙(HLE)循环相交的八个交点中,有四个交点H、B、C、L共线,由六连环定理,另外四个交点P、Q、R、S共圆(不可能共线,因为P在∠NAH内,R在∠KCL内,S在∠LDM内,P、R、S三点不会共线)。同理,Q、R、S、T四点共圆,故P、Q、R、S、T五点共圆[3]。
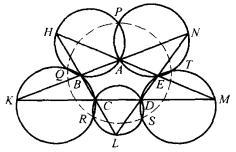 图8
图8



 求购
求购










