空间向量

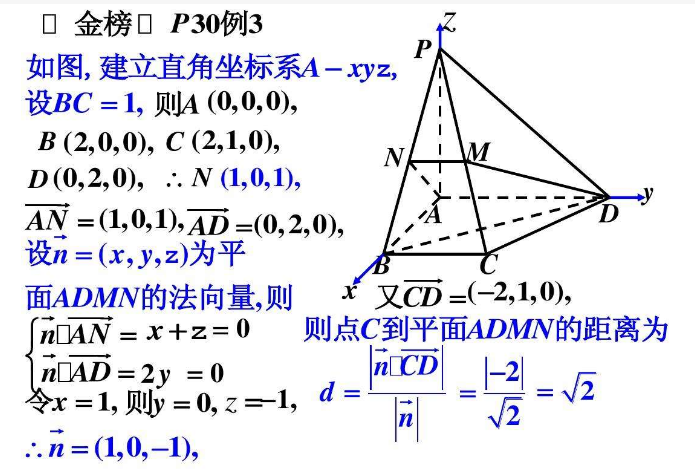空间向量(3)1共线向量定理

两个空间向量 a, b向量( b向量不等于 0）， a∥ b的充要条件是存在唯一的 实数λ，使 a=λ b

2 共面向量定理

如果两个向量 a, b不共线，则向量 c与向量 a, b共面的 充要条件是：存在唯一的一对实数x,y,使 c= ax+ by

3 空间向量分解定理

如果三个向量 a、 b、 c不共面，那么对空间任一向量 p，存在一个唯一的有序实数组x，y，z，使 p=x a+y b+z c。

任意不共面的三个向量都可作为空间的一个基底， 零向量的表示唯一。

以下用向量法求解的简单常识：

1、空间一点P位于平面MAB的充要条件是存在唯一的 有序实数对x、y，使得 PM=x PA+y PB

2、对空间任一点O和不共线的三点A，B，C，若： OP=x OA+y OB+z OC （其中x+y+z=1），则四点P、A、B、C共面．

3、利用向量证a∥b，就是分别在a，b上取向量 a=λ b（λ∈R）．

4、利用向量证a⊥b，就是分别在a，b上取向量 a· b=0 ．

5、利用向量求两直线a与b的夹角，就是分别在a，b上取 a, b，求：< a, b> 的问题．

6、利用向量求距离即求 向量的模问题．

7、利用坐标法研究线面关系或求角和距离，关键是建立正确的 空间直角坐标系，正确表达已知点的坐标．

第一步：

按照图形建立三维坐标系O-xyz 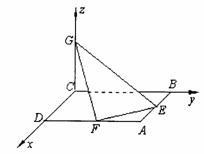空间向量之后，将点的坐标带进去，求出所需向量的坐标。

第二步：

求平面的法向量：

令法向量 n=（x,y,z）

因为法向量垂直于此平面

所以 n垂直于此面内两相交直线（其方向向量为 a， b)

可列出两个方程 n· a=0, n· b=0

两个方程，三个未知数

然后根据计算方便

取z（或x或y）等于一个数（如：1，√2等）

代入即可求出面的一个法向量 n的坐标了.

会求法向量后

1.斜线与平面所成的角就是求出斜线的方向向量与平面的法向量 n的夹角，所求角为上述夹角的余角或者夹角减去π/2.

2.点到平面的距离就是求出该面的法向量 n在平面上任取(除被求点在该平面的射影外）一点，

求出平面外那点和你所取的那点所构成的向量，记为 a

点到平面的距离就是法向量 n与 a的数量积的绝对值| n· a|除以法向量的模| n|即得所求.

3. 二面角的求法就是求出两个平面的法向量

可以求出两个法向量的夹角为两向量的数量积除以两向量模的乘积 ：cos< n,m>=| n· m|/(| n|| m|)

那么二面角就是上面求的两法向量的夹角或者它的补角。

4.设直线l,m的方向向量分别为 a,b，平面α,β的法向量分别为 μ,ν 则

线线平行 l∥m<=> a∥ b <=> a=k b

线面平行 l∥α<=> a⊥ μ <=> a· μ= 0

面面平行 α∥β<=>   μ∥ ν <=> μ=k ν

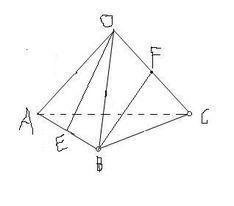空间向量  线线垂直 l⊥m<=> a⊥ b <=> a· b= 0

线面垂直 l⊥α <=> a∥ μ <=> a=k μ

面面垂直 α⊥β<=> μ⊥ ν <=> μ· ν= 0

5.向量的坐标运算：设 a=(x1,y1)， b=(x2,y2)，则

1.| a|=√（x1²+y1²)

2. a+ b=(x1+x2,y1+y2)

3. a- b=(x1-x2,y1-y2)

4.k a=k(x1,y1)=(kx1,ky1)

5. a· b=x1x2+y1y2

6. a∥ b<=> x1y2=x2y1(一般写为：x1y2-x2y1=0)

7. a⊥ b<=> a· b=0<=>x1x2+y1y2=0

8.cos< a, b>=（ a· b）/（| a|·| b|）=(x1x2+y1y2) / [ √(x1²+y1²)·√(x2²+y2²) ]

注：x1中的1为下标，以此类推

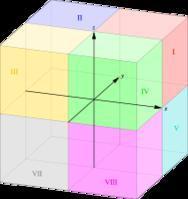空间向量(1)

三个坐标面把 空间分成八个部分，每个部分叫做一个 卦限。含有x轴 正半轴、y轴正半轴、z轴正半轴的卦限称为第一卦限，其他第二、三、四卦限，在xoy面的上方，按 逆时针方向确定。在第一、二、三、四卦限下面的部分分别称为第五、六、七、八卦限。 ^[2]

空间向量(3)立体几何的计算和证明常常涉及到二大问题：一是位置关系，它主要包括线线垂直，线面垂直，线线平行，线面平行；二是度量问题，它主要包括点到线、点到面的距离，线线、线面所成角，面面所成角等。这里比较多的主要是用向量证明线线、线面垂直及计算线线角，而如何用向量证明线面平行，计算点到平面的距离、线面角及面面角的例题不多，起到一个抛砖引玉的作用。