- 流体运动学
流体运动学
流动的分析描述
在流体力学中描写运动的方法有两种,即拉格朗日方法和欧拉方法。拉格朗日方法着眼于流体质点(见连续介质假设),设法描述每个流体质点的位置随时间变化的规律。通常利用初始时刻流体质点的直角坐标或曲线坐标a、b、c作为区分不同流体质点的标志。流体质点运动规律可表示成方程(1)的形式:[1]
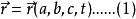
其中![]() 是流体质点的矢径;t为时间;变数a、b、c、t统称为拉格朗日变数。对时间 t求式(1)的一次偏导数和二次偏导数,可分别得到流体质点的速度矢量相加速度矢量。欧拉方法着眼于空间点,设法在空间的每一点上描述出流体运动随时间的变化状况。通常用速度矢量v表示流体运动。于是欧拉方法中流体质点的运动规律可表为下式:
是流体质点的矢径;t为时间;变数a、b、c、t统称为拉格朗日变数。对时间 t求式(1)的一次偏导数和二次偏导数,可分别得到流体质点的速度矢量相加速度矢量。欧拉方法着眼于空间点,设法在空间的每一点上描述出流体运动随时间的变化状况。通常用速度矢量v表示流体运动。于是欧拉方法中流体质点的运动规律可表为下式:
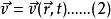
变数![]() 称为欧拉变数。式(2)确定的速度函数是定义在时间t和空间点上的,所以它是场。由式(2),可按下式求出加速度(见随体导数):
称为欧拉变数。式(2)确定的速度函数是定义在时间t和空间点上的,所以它是场。由式(2),可按下式求出加速度(见随体导数):
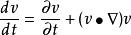
虽然拉格朗日方法和欧拉方法都能描述流体的运动,但在流体力学中,人们广泛采用欧拉方法,较少采用拉格朗日方法,这是因为用欧拉变数得到的是场,可以运用研究得很充分的场论知识;而在拉格朗日方法中,由于式(1)不是场,所以无此优点。其次,在欧拉方法中,由于加速度是一阶导数,所以运动方程组是一阶偏微分方程组,它比拉格朗日方法中的二阶偏微分方程组容易处理。
流动的几何描述
在拉格朗日方法中,流体质点运动规律的几何表示是迹线。在欧拉方法中,则利用流线几何地描述流体的运动。在非定常运动中,流线和迹线一般是不重合的;而在定常运动中,两者必然重合(见流线)。
流动的分析
流体运动要比刚体运动复杂,因为它除了平动和转动外,还要发生变形。流体微团运动分析的主要内容包含在亥姆霍兹速度分解定理中。
流动的分类
运动形式——无旋运动和有旋运动
以运动形式为标准,流体运动可分为无旋运动和有旋运动。若在整个流场中▽×v=0,则称此运动为无旋运动,反之称为有旋运动。
时间为标准——定常运动和非定常运动
以时间为标准,流体运动可分为定常运动和非定常运动。若所有物理量皆不依赖于时间t,则称此运动为定常运动,反之称为非定常运动。
空间标准——一维运动、二维运动和三维运动
以空间为标准,根据有关物理量依赖于一个曲线坐标、二个曲线坐标和三个曲线坐标,流体运动可分为一维
运动、二维运动和三维运动。平面运动和轴对称运动是二维运动的两个重要例子。在直角坐标系Oxyz中,满
足![]() ,
,![]() 的流动称为平面运动,其中w是速度矢量在z轴的分量。在柱坐标系(r,φ,z)中满足
的流动称为平面运动,其中w是速度矢量在z轴的分量。在柱坐标系(r,φ,z)中满足
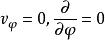
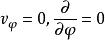 ,或球坐标系(r,φ,θ)中满足的流动称为轴对称运动,其中vφ是速度矢量在φ轴的分量。
,或球坐标系(r,φ,θ)中满足的流动称为轴对称运动,其中vφ是速度矢量在φ轴的分量。
涡旋的运动学性质
涡管的运动学性质为:涡通量在涡管所有横截面上都等于同一常数,称之为涡管的强度。涡管不能在流体内产生或终止,如果它不以涡环的形式存在,就只能延伸到边界上。
区域中有涡和源的分布,就会诱导出速度场。知道涡旋场和散度场求速度场的问题归结为解方程(3):
▽·v=Θ,▽×v=Ω, (3)
式中Θ和Ω是区域内给定的源和涡的强度分布函数。其解为:
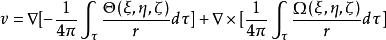 ,
,
式中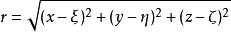 ;
;
ξ、η、ζ是变动点坐标。
连续性方程和流函数
连续性方程是质量守恒定律的数学表达式,它的一般形式为(见流体力学基本方程组):
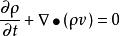 或
或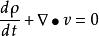
对于定常运动和不可压缩流体,连续性方程可简化为:
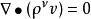
式中v=0和v=1分别对应不可压缩流体和定常运动。对于平面和轴对称运动,由连续性方程推出,存在着流函数Ψ,使
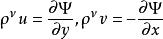 , (平面运动)
, (平面运动)
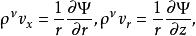 (轴对称运动)
(轴对称运动)
式中u、v,vx、vr分别是速度矢量在直角坐标(x,y,z)和柱坐标(r,φ,z)中的分量。
无旋运动和速度势
根据运动的无旋性▽×v=0推出存在着速度势Φ,使v=▽Φ。在不可压缩流体情形,速度势满足拉普拉斯方程(见拉普拉斯无旋运动,速度势)。

-
新款大众途铠正式上市 豪华加运动
2025-10-31 14:43:40 查看详情 -
捷尼赛思GV60正式上市 新美式运动健将
2025-10-31 14:43:40 查看详情 -
广汽本田全新皓影正式上市 宝马1系M运动曜熠版上市
2025-10-31 14:43:40 查看详情 -
吉利缤越PRO家族正式上市 新款路虎发现运动版海外上市
2025-10-31 14:43:40 查看详情 -
新款路虎发现运动版海外上市 油耗1.3L/100km
2025-10-31 14:43:40 查看详情 -
东风标致新408将于今日发布 最新家族设计/运动风凸显
2025-10-31 14:43:40 查看详情 -
新款吉利嘉际L将于9月3日上市 运动风格明显
2025-10-31 14:43:40 查看详情 -
BMW116i都市版首付三成 运动先锋
2025-10-31 14:43:40 查看详情 -
东风标致全新三厢轿车谍照再度曝光 最新家族设计/运动风凸显
2025-10-31 14:43:40 查看详情 -
2023款吉利星瑞7月18日上市 运动风格明显
2025-10-31 14:43:40 查看详情


 求购
求购

