- 傅里叶积分算子

傅里叶积分算子
中文名
傅里叶积分算子
相关
奇异积分算子
类别
相关词汇
概述
傅里叶积分算子(Fourier integral operator)是偏微分算子理论中的重要工具。它和拟微分算子一起,被称为“70年代技术”。拟微分算子的前身是具强奇性的卷积型奇异积分算子。
傅里叶积分算子产生于用几何光学方法求经典波动过程的渐近表达式及求量子力学问题在大范围内适用的准经典近似。拉克斯1957年关于前一方面的工作,马斯洛夫1965年关于后一方面的工作,导致赫尔曼德尔于1968~1970年期间系统地建立了傅里叶积分算子的局部以及整体理论。
基本原理
设![]() 和
和![]() 分别是
分别是![]() 和
和![]() 中的开集。
中的开集。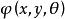 是
是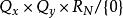 中的实值位相函数。
中的实值位相函数。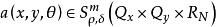 ,
,![]() ,
,![]() 。对于任一
。对于任一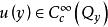 ,作
,作
![]() 其中
其中
![]() 是一个振荡积分。由
是一个振荡积分。由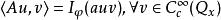 式子确定的
式子确定的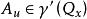 。这样,就确定了一个线性算子
。这样,就确定了一个线性算子
![]() 这个算子称为傅里叶(Fourier)积分算子。
这个算子称为傅里叶(Fourier)积分算子。
由此知,傅里叶(Fourier)积分算子![]() 所对应的分布核
所对应的分布核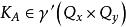 由下式确定
由下式确定
![]()
![]() 显见,此分布核是一个傅里叶(Fourier)分布。有时,我们也用同一记号
显见,此分布核是一个傅里叶(Fourier)分布。有时,我们也用同一记号![]() 表示此分布核。[1]
表示此分布核。[1]

相关百科
-
比例积分电动三通调节阀
2025-09-14 05:04:48 查看详情 -
加油卡怎么使用(邮政积分兑换加油卡怎么使用)
2025-09-14 05:04:48 查看详情 -
新款沃尔沃XC90上市 都是积分惹的祸
2025-09-14 05:04:48 查看详情 -
疑似沃尔沃EX30谍照首曝 都是积分惹的祸
2025-09-14 05:04:48 查看详情 -
沃尔沃EX30最新消息 都是积分惹的祸
2025-09-14 05:04:48 查看详情 -
沃尔沃P1800电动车谍照 都是积分惹的祸
2025-09-14 05:04:48 查看详情 -
沃尔沃EX90最新预告图 都是积分惹的祸
2025-09-14 05:04:48 查看详情


 求购
求购



