- 拉盖尔多项式
拉盖尔多项式
前几个拉盖尔多项式
前几个拉盖尔多项式的表达式与函数图像如下:
| n | |
| 0 | |
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 |
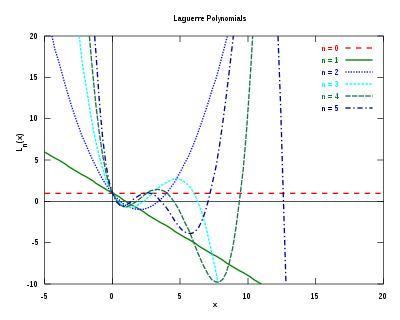 前六个拉盖尔多项式
前六个拉盖尔多项式
递归定义
| n | |
| 0 | |
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 |
广义拉盖尔多项式
拉盖尔多项式也可以通过递归的方式进行定义。首先,规定前两个拉盖尔多项式为:
然后运用下面的递推关系得到更高阶的多项式。
广义拉盖尔多项式的性质与应用
上面提到的拉盖尔多项式的正交性,也可以用另外一种方式表达。即:如果X是一个服从指数分布的随机变量(即,概率密度函数如下式):
那么:
指数分布不是唯一的伽玛分布,对于任意的伽玛分布(概率密度函数如下,α > −1,参见Γ函数)
相应的正交多项式为形如下式的广义拉盖尔多项式(可以通过罗德里格公式得到):
有时也将上面的多项式称为连带(联属,伴随)拉盖尔多项式。当取α = 0时,就回到拉盖尔多项式:
递推关系
拉盖尔函数可以由合流超几何函数和Kummer变换得到:
当
为整数时,截断为
阶拉盖尔多项式。
阶拉盖尔多项式可以通过将莱布尼茨乘积求导公式应用在罗德里格公式上而得到,结果为
。
n阶拉盖尔多项式的首项系数为(−1)n/n!;
拉盖尔多项式在x=0的取值(常数项)为
Ln(α)有n个实的正根(应该注意到 构成以施图姆序列),且这些根全部位于区间
中。
当很大,而
不变,
时,拉盖尔多项式的渐近行为如下:
,以及
。
前几个广义拉盖尔多项式为:
根据拉盖尔多项式的定义,可以使用秦九韶算法计算拉盖尔多项式,程序代码如下:
function LaguerreL(n, alpha, x) { LaguerreL:= 1; bin:= 1 for i:= n to 1 step -1 { bin:= bin* (alpha+ i)/ (n+ 1- i) LaguerreL:= bin- x* LaguerreL/ i } return LaguerreL; }拉盖尔多项式的导函数
拉盖尔多项式满足以下的递推关系:
特别地,有
以及
,或
还有
运用以上式子可以得到以下四条关系式:
or
将它们组合在一起,就得到了最常用的递推关系式:
当与
均为整数时,拉盖尔多项式有以下的有趣性质:
进一步可以得到部分分式分解:
正交性
将拉盖尔多项式对自变量x求导k次,得到:
进一步有:
运用柯西多重积分公式可以得到:
将拉盖尔多项式对参变量求导,得到下面的有意思的结果:
广义拉盖尔多项式满足下面的微分方程:
可以与拉盖尔多项式的k阶导数所满足的微分方程作一比较。
仅在此式中,(后面这个符号又有了新的含义)。
于是,当时,广义拉盖尔多项式可以用拉盖尔多项式的导数表示:
式中的上标(k)容易与求导k次混淆。
级数展开
伴随拉盖尔多项式在区间[0, ∞)上以权函数xα e −x正交:
这可由下式得到:
伴随对称核多项式可以用拉盖尔多项式表示为:
也有下面的递推关系:
进一步地,在伴L2[0, ∞)空间上,有:
在氢原子的量子力学处理中用到了下面的公式:
围道积分表示
设一个函数具有以下的级数展开形式:
则展开式的系数由下式给出
这个级数在Lp空间上收敛,当且仅当
一个相关的展开式为:
特别地
这可由下式得到:
还有,当时,
这个结果可以由下式导出,
幂函数可以展开为:
二项式可以展开为:
进一步可以得到:
(当且仅当
时收敛)
更一般地
对于非负的整数,可以化简为:
当时,可以化简为:
或
雅可比Theta 函数有下面的表示:
随意选定参量t,贝塞尔函数可以表示为:Γ函数可以展开为:
低阶不完全伽玛函数可展开为:
还有:
于是,高阶不完全伽玛函数就是:
表示超几何函数。
与埃尔米特多项式的关系
拉盖尔多项式可以用围道积分表示,如下式所示:
积分方向逆时针绕原点一周。
与超几何函数的关系
广义拉盖尔多项式与埃尔米特多项式有下列关系:
以及
这里的Hn表示乘上了exp(−x2)的埃尔米特多项式(所谓的“物理学家形式”)。正因为这样,广义拉盖尔多项式也在量子谐振子的量子力学处理中出现。
与贝塞尔函数的关系
拉盖尔多项式可以用超几何函数来定义,具体地说,是用合流超几何函数定义:
是阶乘幂,这里表示升阶乘。

-
将于3月24日上市 整车多项升级/搭载双激光雷达
2025-09-22 15:29:48 查看详情 -
小鹏全新P7i将于今日上市 整车多项升级/搭载双激光雷达
2025-09-22 15:29:48 查看详情 -
上海车展上市 整车多项升级/搭载双激光雷达
2025-09-22 15:29:48 查看详情 -
2004款奥迪A4中央扶手箱盖按装方法(奥迪扶手箱扣如何安装)
2025-09-22 15:29:48 查看详情 -
奥迪A6L音响如何拆装(奥迪后门高音盖怎么拆)
2025-09-22 15:29:48 查看详情 -
奥迪a4l机顶盖如何盖上(奥迪a4l机顶盖怎么盖上)
2025-09-22 15:29:48 查看详情 -
奥迪a3气囊盖更换步骤(奥迪a3气囊盖更换步骤介绍)
2025-09-22 15:29:48 查看详情


 求购
求购




