稠密集

在度量空间(E,d)中，也可以如下定义稠密集。当X的拓扑由一个度量给定时，在X中A的闭包是A与A中元素的所有数列极限（它的极限点）的集合的并集，

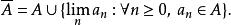
那么当

A在X中是稠密的。

注意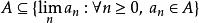。如果是一个完备度量空间X中稠密开集上的序列，则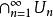在X上依然稠密。这个事实与贝尔纲定理中的一个形式等价。^[1][2]

1.每一拓扑空间是其自身的稠密集。

2.有理数域和无理数域是实数域中的稠密集（在通常拓扑意义下）。

3.度量空间M是其完备集γM中的稠密集。^[1]