- 卡尔·龙格
卡尔·龙格
基本信息
| 出生 | 1856年8月30日(1856-08-30)德国不来梅 |
|---|---|
| 逝世 | 1927年1月3日 (70岁)德国哥廷根 |
| 居住地 | 德国 |
| 公民权 | 德国人 |
| 国籍 | 德国 |
| 研究领域 | 数学,物理学 |
| 任职于 | 汉诺威莱布尼兹大学(1886 年-1904 年)哥廷根大学(1904 年-1925 年) |
| 母校 | 柏林大学 |
| 博士导师 | 卡尔·魏尔施特拉斯,Ernst Kummer |
| 博士学生 | 马克斯·玻恩 |
| 著名成就 | 龙格-库塔法,龙格现象,拉普拉斯-龙格-楞次矢量 |
人物生平
| 出生 | 1856年8月30日(1856-08-30)德国不来梅 |
|---|---|
| 逝世 | 1927年1月3日 (70岁)德国哥廷根 |
| 居住地 | 德国 |
| 公民权 | 德国人 |
| 国籍 | 德国 |
| 研究领域 | 数学,物理学 |
| 任职于 | 汉诺威莱布尼兹大学(1886 年-1904 年)哥廷根大学(1904 年-1925 年) |
| 母校 | 柏林大学 |
| 博士导师 | 卡尔·魏尔施特拉斯,Ernst Kummer |
| 博士学生 | 马克斯·玻恩 |
| 著名成就 | 龙格-库塔法,龙格现象,拉普拉斯-龙格-楞次矢量 |
龙格库塔法
 卡尔·龙格肖像卡尔·龙格(CarlRunge1856年8月30日-1927年1月2日)
卡尔·龙格肖像卡尔·龙格(CarlRunge1856年8月30日-1927年1月2日)
1880 年,他得到柏林大学的数学博士,是著名德国数学家,被誉为“现代分析之父”的卡尔·魏尔施特拉斯的学生。1886 年,他成为在德国汉诺威的汉诺威莱布尼兹大学的教授。
他的兴趣包括数学,光谱学,大地测量学,与天体物理学。除了纯数学以外,他也从事很多涉及实验的工作。他跟海因里希·凯瑟一同研究各种元素的谱线,又将研究的结果应用在天体光谱学。
1904 年,因为哥廷根大学教授,菲利克斯·克莱因的主动邀请,他同意去那里教书。1925 年,他在哥廷根大学退休。
月球的龙格陨石坑(Runge crater) 是因他而命名的。
经典四阶龙格库塔法
数值分析中,龙格-库塔法(Runge-Kutta)是用于模拟常微分方程的解的重要的一类隐式或显式迭代法。这些技术由数学家卡尔·龙格和马丁·威尔海姆·库塔于1900年左右发明。
龙格现象
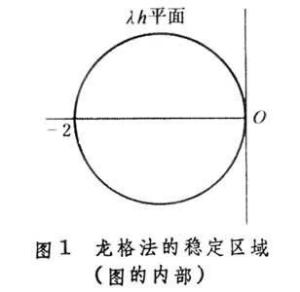 龙格法的稳定区域对于一阶精度的欧拉公式有:
龙格法的稳定区域对于一阶精度的欧拉公式有:
yi+1=yi+h*K1 K1=f(xi,yi)
当用点xi处的斜率近似值K1与右端点xi+1处的斜率K2的算术平均值作为平均斜率K*的近似值,那么就会得到二阶精度的改进欧拉公式:
yi+1=yi+h*( K1+ K2)/2
K1=f(xi,yi)
K2=f(xi+h,yi+h*K1)
依次类推,如果在区间[xi,xi+1]内多预估几个点上的斜率值K1、K2、……Km,并用他们的加权平均数作为平均斜率K*的近似值,显然能构造出具有很高精度的高阶计算公式。经数学推导、求解,可以得出四阶龙格-库塔公式,也就是在工程中应用广泛的经典龙格-库塔算法:
yi+1=yi+h*( K1+ 2*K2 +2*K3+ K4)/6
K1=f(xi,yi)
K2=f(xi+h/2,yi+h*K1/2)
K3=f(xi+h/2,yi+h*K2/2)
K4=f(xi+h,yi+h*K3)
通常所说的龙格-库塔法是指四阶而言的,我们可以仿二阶、三阶的情形推导出常用的标准四阶龙格-库塔法公式。龙格-库塔法具有精度高,收敛,稳定(在一定条件下),计算过程中可以改变步长,不需要计算高阶导数等优点,但仍需计算 在一些点上的值,如四阶龙格-库塔法每计算一步需要计算四次 的值,这给实际计算带来一定的复杂性,因此,多用来计算“表头”。
拉普拉斯龙格楞次矢量
 龙格现象在计算方法中,有利用多项式对某一函数的近似逼近,这样,利用多项式就可以计算相应的函数值。例如,在事先不知道某一函数的具体形式的情况下,只能测量得知某一些分散的函数值。例如我们不知道气温随日期变化的具体函数关系,但是我们可以测量一些孤立的日期的气温值,并假定此气温随日期变化的函数满足某一多项式。这样,利用已经测的数据,应用待定系数法便可以求得一个多项式函数f(x)。应用此函数就可以计算或者说预测其他日期的气温值。一般情况下,多项式的次数越多,需要的数据就越多,而预测也就越准确。例外发生了:龙格在研究多项式插值的时候,发现有的情况下,并非取节点(日期数)越多多项式就越精确。著名的例子是f(x)=1/(1+25x^2).它的插值函数在两个端点处发生剧烈的波动,造成较大的误差。究其原因,是舍入误差造成的。
龙格现象在计算方法中,有利用多项式对某一函数的近似逼近,这样,利用多项式就可以计算相应的函数值。例如,在事先不知道某一函数的具体形式的情况下,只能测量得知某一些分散的函数值。例如我们不知道气温随日期变化的具体函数关系,但是我们可以测量一些孤立的日期的气温值,并假定此气温随日期变化的函数满足某一多项式。这样,利用已经测的数据,应用待定系数法便可以求得一个多项式函数f(x)。应用此函数就可以计算或者说预测其他日期的气温值。一般情况下,多项式的次数越多,需要的数据就越多,而预测也就越准确。例外发生了:龙格在研究多项式插值的时候,发现有的情况下,并非取节点(日期数)越多多项式就越精确。著名的例子是f(x)=1/(1+25x^2).它的插值函数在两个端点处发生剧烈的波动,造成较大的误差。究其原因,是舍入误差造成的。
具体的情况可参考下列Mathematica程序:
n = 10; x = Range[-1, 1, 2/n]; y = 1./(1 + 25 x^2);
p =Transpose[{x, y}]; Clear[t];
f = LagrangeInterpolation[x, y, t];
Show[ Plot[{1./(1 + 25 t^2), f}, {t, -1, 1}], ListPlot[p, PlotStyle -> PointSize[0.02]] ]

-
卡尔·弗里德里希·本茨
2025-09-21 12:51:57 查看详情


 求购
求购










