- 对数线性模型
对数线性模型
简介
对数线性模型描述的是概率与协变量之间的关系;对数线性模型也用来描述期望频数与协变量之间的关系。
考虑期望频数m的取值范围在0到无穷之间,故需要进行对数变换为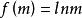 ,使它的取值在
,使它的取值在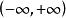 之间。
之间。
对数线性模型具有以下形式:
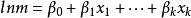
不过,与logit不同的是,对数模型中没有解释变量,是用行列因子的效应参数来表示。[1][2][3]
对数线性模型基本思想
对数线性模型分析是把列联表资料的网格频数的对数表示为各变量及其交互效应的线性模型,然后运用类似方差分析的基本思想,以及逻辑变换来检验各变量及其交互效应的作用大小。
列联表
(1)作用:分析定类变量和定类变量之间有无关系;
(2)优缺点:不需要确定因变量和自变量。但是,卡方检验对三维和三维以上列联表资料的分析有一定困难,即对混杂变量的控制较难。约束条件少、清晰、可以快速准确进行判断。失去了对多变量之间的交互联系的分析,进行两变量间关联分析时缺乏统计控制,不能准确定量描述一个变量对另一个变量的作用幅度。
(3)列联表的四种类型:
双向无序列联表;
单向有序列联表;
双向有序且属性不同的列联表;
双向有序且属性相同的列联表。[4]
逻辑回归
(1)作用:分析尺度变量(也可引入类别变量)与二分类别变量之间的因果关系;
(2)优缺点:解决了对混杂变量的控制的问题,而且,它能将因变量与自变量的关系用模型表示出来,清晰易理解。但是,当模型中自变量较多,特别是名义变量较多,或名义变量的类别较多时,分析自变量之间的交互效应就很繁杂,可能需要建立很多哑变量。
对数线性模型
(1)作用:综合运用方差分析和逻辑回归中的建模方法,应用于纯粹定类变量之间,系统评价各变量间关系和交互作用大小的多元统计方法;
(2)优缺点:可以直接分析各种类型的分类变量,对于名义变量,也不需要事先建立哑变量,可以直接分析变量的主效应和交互效应。对数线性模型不仅可以解决卡方分析中常遇到的高维列联表的“压缩”问题,又可以解决logistic回归分析中多个自变量的交互效应问题。
二维对数线性模型
公式
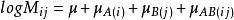
其中,![]() 为总均值,
为总均值,![]() 主效应A,
主效应A,![]() 主效应B,
主效应B,![]() 交互效应AB。
交互效应AB。![]() 为第i行第j列网格频数的理论值或期望频数值(expected ferquency)。
为第i行第j列网格频数的理论值或期望频数值(expected ferquency)。
限制条件:
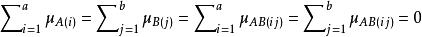
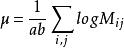
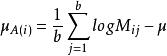
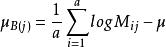
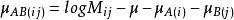
二维对数线性模型的分类
1、一阶交互效应模型
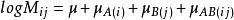
2、完全独立模型
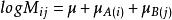
三维对数线性模型
公式
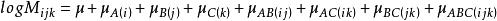
其中,![]() 为总均值,
为总均值,![]() 主效应A,
主效应A,![]() 主效应B,,
主效应B,,![]() 主效应C,
主效应C,![]() 等为交互效应。
等为交互效应。![]() 为第i行第j列网格频数的理论值或期望频数值(expected ferquency)。
为第i行第j列网格频数的理论值或期望频数值(expected ferquency)。
三维对数线性模型的分类
1、二阶交互效应模型
2、无二阶交互效应模型
3、条件独立模型
4、联合独立模型
5、完全独立模型
对数线性模型的基本原理
与方差分析相关的
在多元方差分析中,以二元方差为例:每一个观测值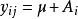 的效果+
的效果+![]() 的效果+
的效果+![]() 交互作用+Ɛij。
交互作用+Ɛij。
比数比
比数比是对数线性模型的基础,而比数比又是由比数计算而来。那么什么叫做比数呢?比数是一个事件发生的概率与其不发生概率之比,测量了一个事件发生的可能性。这个数值越高说明结果2相对于结果1发生的可能性就越高。
与逻辑变换有关的
令R表示行,C表示列,![]() 表示第i行第j列的观测频次。那么期望频次
表示第i行第j列的观测频次。那么期望频次![]() 被设定为一个乘积的函数
被设定为一个乘积的函数
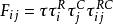
![]() 代表概率里面的总概率值1,
代表概率里面的总概率值1,![]() 和
和![]() 分别代表R和C的边缘效应,
分别代表R和C的边缘效应,![]() 代表R与C的二维交互效应,而交互效应实质上测量的就是R与C之间的比数比,当
代表R与C的二维交互效应,而交互效应实质上测量的就是R与C之间的比数比,当![]() =1的时候就是我们熟悉的独立模型。 ò相乘形式的不好计算,我们将其取对数。[5]
=1的时候就是我们熟悉的独立模型。 ò相乘形式的不好计算,我们将其取对数。[5]
对数线性模型的假设检验
假设检验的作用
统计推论中包括参数估计与假设检验两部分,上面我们已经介绍了参数估计,那估计的可信度有多少,还要经过假设检验。不经过统计检验,研究者便不能肯定得到的参数估计是不是仅仅源于抽样误差,因而不能肯定在总体中是否存在相同情况。所有结论只能限于这个样本之内,不能肯定再抽一个样本能否得到类似结果。
统计量
似然卡方比,根据相关计算,看原假设是否成立。
贝叶斯信息标准,不同模型而言越小的BIC越好。
对数线性模型的统计检验
四种主要检验:
1、对于假设模型的整体检验;
2、分层效应的检验;
3、单项效应的检验;
4、单个参数估计的检验。
对于假设模型的整体检验
采用似然比卡方检验(likelihood-ratio chi-square test,标为L2)
在样本量较大时, L2与皮尔逊卡方统计量的值十分接近。 L2优越性:
1、期望频数采用似然估计方法,因而更加稳健;
2、可以被分解成若干部分,即各项效应都有对应的似然卡方值,并且它们的似然卡方值之和等于整个模型的似然卡方比值。
公式:
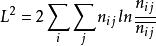
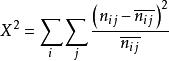
其中![]() 为估计交互频数。
为估计交互频数。
整体检验的不足之处:
整体检验显著只能说明撤销的效应项中起码有一项是有显著作用的,但不能确定是哪一项显著。所以,整体检验在实际对数线性模型分析中,主要服务于整个检验模型的检验情况,而确定各项效应时则是通过单项效应的检验。且对于一个多阶多项效应的复杂模型,采用整体检验方式就意味着逐项效应的剔除测试,这样分析过程效率太低。
分层效应检验
当研究中涉及的因素较多时,不仅主效应项会增加,交互效应项增加得更快。例如,四个因素的模型,主效应4个,二阶交互效应6项,三阶交互效应4项,四阶交互效应1项。如此,逐项检验筛选重要目标就太繁琐了。 且在一般情况下,高阶交互效应不太容易显著。因此采用按阶次集体检验交互效应项的方法十分间接有效。
分层效应检验有两种:
一、某一阶及更高阶所有交互效应项的集体检验,它的检验是否显著表明这一阶及以上各阶中是否至少有一项是重要的;
二、某一阶所有交互效应的集体检验,它的检验是否显著表明这一阶所有交互效应中是否至少有一项是重要的。 ò前者检验比后者综合性更强。
分层效应检验的不足:
整体检验或分层检验的结果只能说明所有效应中或某一组效应中至少有一项效应具有显著重要影响。但并不能明确知道究竟是哪一项显著。
为了了解到底是哪些具体项目显著,还需要采用单项效应的单独检验。
单项效应的检验
SPSS的单项效应检验只是在分层模型中对饱和模型分析时提供。它反映的是如果从模型中撤销一个效应以后对L2变化的检验,称为偏关联检验(tests of PARTIAL associations)。
单项效应检验的不足:
在制定对数线性模型时,一个因素中可能不只两个类别。单项效应检验只是肯定这项效应中起码有一类与其他类存在明显差别,但并不能提供究竟是哪一类。
因此,需要利用单个参数估计的检验来解决这个问题。
单个参数估计的检验
均为二类的情况下,参数估计的绝对值相同、各参数估计标准误相同,因此它们的Z检验值的绝对值相同,因此他们的显著性水平也相同。 如果是三类或者三类以上,经过单项偏关联检验显著或经筛选保留的交互项中,不一定所有参数都是显著的。[6]

-
非线性方程组数值解法
2025-09-28 09:24:21 查看详情 -
非线性阈值协整理论及其在中国的应用研究
2025-09-28 09:24:21 查看详情


 求购
求购









