- 距离空间

距离空间
定义
设X是非空集合,对于X中任意的两个元素x与y,按某一法则都对应唯一的实数d(x,y),而且满足下述三条公理:
(1)(非负性)d(x,y)≥0,[d(x,y)=0,当且仅当x=y];
(2)(对称性)d(x,y)=d(y,x);
(3)(三角不等式)对于任意的x,y,z∈X,恒有d(x,y)≤d(x,z)+d(z,y)。
则称d(x,y)为x与y的距离,并称X是以d为距离的距离空间,记作(X,d)。通常,在距离已被定义的情况下,(X,d)可以简单地将X中的元素称为X中的点[1]。
点集
这里用抽象的距离![]() 代替R中的绝对值
代替R中的绝对值![]() ,用开球
,用开球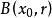 代替R中的对称开区间
代替R中的对称开区间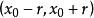 。
。
设(X,d)为距离空间,则可依次定义概念[1]:
开球
设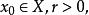 称X中的点集
称X中的点集
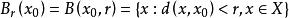 是以
是以![]() 为中心,以
为中心,以![]() 为半径的开球;又称为
为半径的开球;又称为![]() 的
的![]() 邻域。
邻域。
闭球
设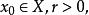 称
称
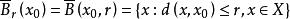 是以
是以![]() 为中心,以
为中心,以![]() 为半径的闭球。
为半径的闭球。
球面
设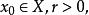 称
称
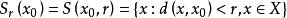 是以
是以![]() 点为中心,以
点为中心,以![]() 为半径的球面。
为半径的球面。
内点
设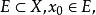 若存在
若存在![]() 的
的![]() 邻域
邻域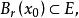 则称点
则称点![]() 为E的内点,E的内点全体称为E的内部记为E。
为E的内点,E的内点全体称为E的内部记为E。
开集
设![]() 若G中每一点都是其内点,则称G为开集。
若G中每一点都是其内点,则称G为开集。
闭集
设![]() 若
若![]() 为开集,则称F为闭集。
为开集,则称F为闭集。
邻域
包含![]() 的任一开集均称为
的任一开集均称为![]() 的一个邻域,特别称
的一个邻域,特别称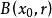 是
是![]() 的球形邻域,有时也简称邻域。
的球形邻域,有时也简称邻域。
聚点
设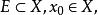 若
若![]() 的每一个邻域中均含有E的无穷多个点,则称
的每一个邻域中均含有E的无穷多个点,则称![]() 为E的聚点或极限点,E的聚点可以在E中也可不在E中,
为E的聚点或极限点,E的聚点可以在E中也可不在E中,![]() 为E的聚点可等价定义为:
为E的聚点可等价定义为:![]() 的每个邻域中含有E的点x,但
的每个邻域中含有E的点x,但![]() 。
。
导集
E的聚点的全体称为E的导集,记为![]() 。
。
闭包
设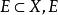 的闭包
的闭包![]() 定义为
定义为![]()
![]() 中的点又称为E的接触点。可以知道
中的点又称为E的接触点。可以知道![]() 的充要条件是
的充要条件是![]() 因此E的闭包
因此E的闭包![]() 又可定义为与E的距离为0的一切点的全体,E的聚点(极限点)必是E的接触点,反之则不然。
又可定义为与E的距离为0的一切点的全体,E的聚点(极限点)必是E的接触点,反之则不然。
孤立点
、边界、有界集、直径
若用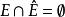 不含在E中的E的聚点集合,则有
不含在E中的E的聚点集合,则有
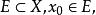 (其中
(其中![]() ).
).
设![]() 若
若![]() 的某一邻域中没有除
的某一邻域中没有除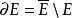 以外的E的其他点,则称
以外的E的其他点,则称![]() 为E的孤立点。称
为E的孤立点。称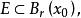 为E的边界;设
为E的边界;设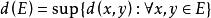 若
若![]() 则称E为有界集;称
则称E为有界集;称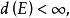 为E的直径,如果 的直径 ,则E是有界集[1]。
为E的直径,如果 的直径 ,则E是有界集[1]。

-
实拍江铃新宝典(图文) 空间满足家用
2025-11-01 05:23:31 查看详情 -
江铃域虎7商乘全能铸就经典 空间满足家用
2025-11-01 05:23:31 查看详情 -
江铃福特轻客持续打造最优TCO 空间满足家用
2025-11-01 05:23:31 查看详情 -
航天恒星空间技术应用有限公司
2025-11-01 05:23:31 查看详情 -
上海车展实拍江铃福特领裕 空间满足家用
2025-11-01 05:23:31 查看详情


 求购
求购




