- 正弦公式
正弦公式
定义
正弦公式是三角学中的一个公式。它指出：对于任意
，
、
、
分别为
、
、
的对边，
为
的外接圆半径，则有
公式证明
证明一
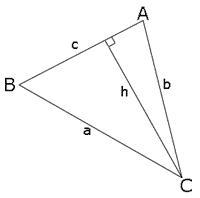图1.余弦公式证明方法一做一个边长为a，b，c的三角形，对应角分别是A，B，C。从向c边做垂线，得到一个长度为h的垂线和两个直角三角形。
很明显：
且
因此：
同理：
证明二
作三角形ABC的外接圆，设半径为R，BC=a
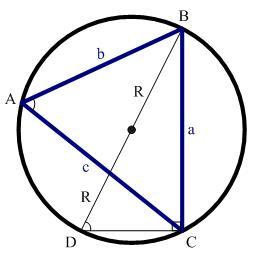图2.余弦公式证明-锐角时1) 角A为锐角时
由于∠A与∠D所对的弧都为BC，根据圆周角定理可了解道
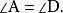
由于BD为外接圆直径，
所以
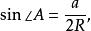
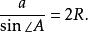
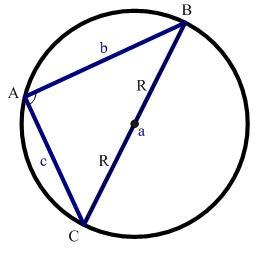图3.余弦公式证明-直角时2）角A为直角时
因为BC =a= 2R，可以得到
所以可以证明，
3)角A为钝角时
线段BD是圆的直径，根据圆内接四边形对角互补的性质，
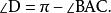
所以
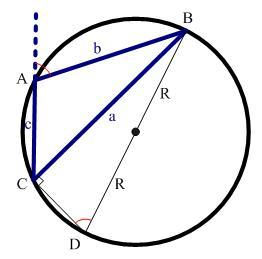图4.余弦公式证明-钝角时
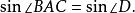
因为BD为外接圆的直径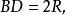
根据正弦定义
变形可得
根据以上的证明方法可以证明得到得到三角形的一条边与其对角的正弦值的比等于外接圆的直径，即
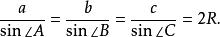
意义
正弦公式指出了任意三角形中三条边与对应角的正弦值之间的一个关系式。
公式应用
三面角正弦定理
若三面角的三个面角分别为α、β、γ，它们所对的二面角分别为A、B、C,则
多边形的正弦关系
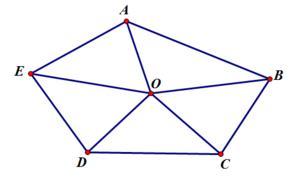图6.多边形的正弦关系
相关百科
-
-
-
-
-
油耗怎么计算（油耗怎么计算公式多少钱一公里）
2025-09-23 13:29:24 查看详情 -
百公里油耗多少钱（百公里油耗多少钱怎么算公式）
2025-09-23 13:29:24 查看详情 -
怎么算油费（怎么算油费公式）
2025-09-23 13:29:24 查看详情 -
汽车油耗怎样计算（汽车油耗怎样计算公式）
2025-09-23 13:29:24 查看详情 -
-
求购