假塑性

（pseudoplastic）

幂律流体（英语：power-law fluid）是一类非牛顿流体，其剪应力τ可表示为

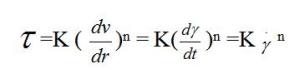
其中，

• K为稠度指数（flow consistency index）
• 为剪切速率（shear rate）
• n为流动特性指数（flow behaviour index）

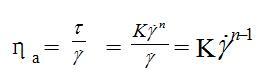
表观粘度（apparent viscosity）或有效粘度（effective viscosity）则可表示为：

上述关系式又被称为奥斯特瓦尔德－德沃尔幂律关系（Ostwald–de Waele power law）。

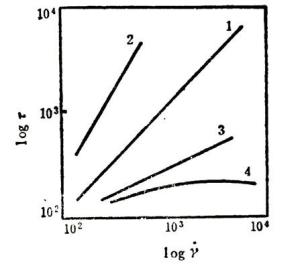不同类型液体的㏒τ～㏒关系

幂律流体可以根据流动特性指数n取值的不同而分为三类：

• n<1：假塑性流体（剪切稀化流体）

n=1：牛顿流体1-牛顿液体,斜率n=1

• n>1：胀流性流体（剪切增稠流体）1-牛顿液体,斜率n=1;2-膨胀性液体(服从指数定律),n>1;3-假塑性液体(服从指数定律),n<1;4-假塑性液体(不服从指数定律),n<1.
• 幂律方程是一种较能反应粘性液体流变性质的经验性数学关系式，它在有限的范围内（剪切速率在一个数量级范围内）有相当好的准确性，并且具有形式简单,使用方便的特点,目前应用最广。对一定的成型加工过程来说，剪切速率总不可能很宽，因此，指数定律在分析液体流变行为、加工能量的计算以及加工设备或模具的设计等方面都比较成功。但是,这个方程有明显的 缺陷,它不能预计低剪切速率和高剪切速率下的恒定粘度,而这恰恰是所有假塑性流体的 物理特征。因此,幂律方程只适用于在中等剪切速率范围内描述假塑性流体的流变特性。

非牛顿（式）流体

是一种流体力学中的概念，与牛顿流体相对（如沥青，熔融状态的塑料，聚合物溶液，悬浮液（比如血液））。作用于液体微元上的摩擦应力除与当前的运动状态外还与液体过去的运动状态有关，也就是说，此种液体有记忆效应。

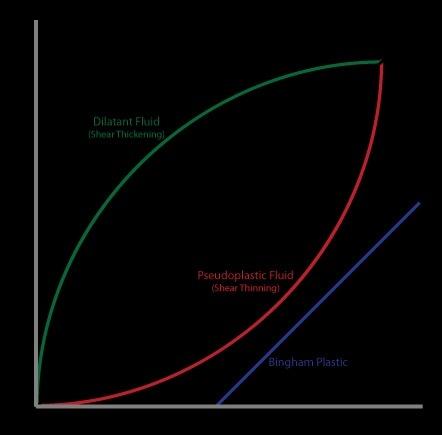
四种类型流体

牛顿流体、剪切增稠流体、假塑性流体、宾汉流体其剪应力与剪应变率之间的关系如上图所示。

非牛顿流体可以分为纯粘性与粘弹性两类：

• 纯粘性非牛顿流体
• 非时变性：如剪切增稠流体（胀流性）、剪切稀化流体（假塑性）
• 时变性：如震凝性流体、触变性流体，即时间依赖性，时间依赖性液体是与假塑性或膨胀型液体有相似性质的另一类聚合物液体，这种液体在流动时的应变和粘度不仅与剪应力或剪切速率的大小有关，而且还与应力作用的时间有关。此外应力在某些时间依赖性液体中引起的应变还表现出滞后效应，说明时间依赖性液体的应变与剪切历史有关，液体表现出粘弹性。定温下表观粘度随剪切持续时间而降低的液体称为触变性液体；相反，表观粘度剪切持续时间而增大的液体为震凝性液体。
• 粘弹性非牛顿流体：这是一类在粘性流动中弹性行为已不能忽视的液体，例如聚苯乙烯、聚甲基丙烯酸甲酯以及聚苯乙烯熔体等。液体中弹性行为是流动过程中聚合物大分子构象改变（蜷曲变为伸展）所引起，大分子伸展贮存了弹性能大分子恢复原来蜷曲构象的过程就引起高弹形变并释放弹性能。流动液体中弹性形变与聚合物的分子量，外力作用的速度或时间以及熔体的温度等有关。一般，随分子量增大，外力作用时间缩短（或作用速度加快）以及当熔体的温度稍高于材料的熔点时，弹性现象表现特别显著。聚合物挤出过程中的出口膨胀就是一种典型的弹性效应。^[1]

1. ^e.g. G. W. Scott Blairet al.,J. Phys. Chem., (1939) 43 (7) 853–864. Also thede Waele-Ostwaldlaw, e.g Markus Reineret al.,Kolloid Zeitschrift(1933) 65 (1) 44-62
2. ^Ostwald called it the de Waele-Ostwald equation:Kolloid Zeitschrift(1929) 47 (2) 176-187