抛物型偏微分方程

抛物型偏微分方程组简称抛物型方程组 (system of parabolic equations,parabolic system)。对于抛物型方程组，一般来说，最大值原理和比较原理并不成立。

先定义二阶抛物线方程组，仅以散度型的二阶线性方程组为例。记 u=（u₁,...,u_k），

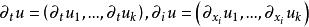设 Q 是中的一个集合，并且对于每一个正整数组（i，j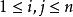），，A_ij(x,t) 是定义在 Q 上的矩阵。考虑下面的二阶线性偏微分方程组：

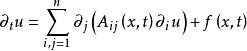(1)

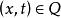如果对任意的和任意的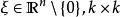矩阵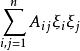的谱都位于右半平面，即谱的实部大于零，则称方程组（1）在 Q 上是二阶线性抛物型方程组。

高阶抛物型方程组的定义比较复杂，下面仅介绍高阶偏导数项不耦合的方程组。

假设对于 i=1,...,k，关于 u_i的偏微分方程

是 2m_i阶抛物型方程，其中，是整数。这时，称偏微分方程组

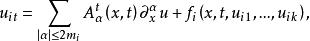
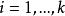
是抛物型方程组，其中

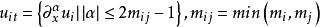对于一个抛物型方程组，如果每个方程式中耦合最多是未知函数的耦合，而没有未知函数的偏导数的耦合，就称这样的抛物型方程组为弱耦合，否则称为强耦合。

例如，方程组

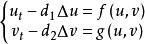是一个耦合抛物型方程组，这里 d₁,d₂>0。下面的方程组

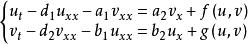是一个强耦合抛物型方程组，其中a₁,a₂,b₁,b₂中至少有一个不为零，这里 d₁,d₂> 0。^[1]