二阶导数

二阶导数记作即y''=（y'）'。^[1]

例如：y=x²的导数为y'=2x，二阶导数即y'=2x的导数为y''=2。

二阶导数(3)（1）切线斜率变化的速度，表示的是一阶导数的变化率。

（2）函数的凹凸性（例如加速度的方向总是指向轨迹曲线凹的一侧）。^[1]

这里以物理学中的瞬时加速度为例:

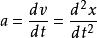根据定义有

可如果加速度并不是恒定的，某点的加速度表达式就为：

a=limΔt→0 Δv/Δt=dv/dt(即速度对时间的一阶导数)

又因为v=dx/dt 所以就有：

a=dv/dt=d²x/dt² 即元位移对时间的二阶导数

将这种思想应用到函数中 即是数学所谓的二阶导数

f'(x)=dy/dx (f(x)的一阶导数）

f''(x)=d²y/dx²=d(dy/dx)/dx (f(x)的二阶导数)

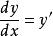设,则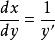，应视为y的函数^[1]

则

=（定义）

=

=（复合函数求导，x是中间变量）

=

=

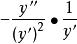
所以，反函数的二阶导数不是原函数二阶导数的倒数。

（1）如果一个函数f(x)在某个区间I上有f''(x)（即二阶导数）>0恒成立，那么对于区间I上的任意x,y，总有：

f(x)+f(y)≥2f[(x+y)/2]，如果总有f''(x)<0成立，那么上式的不等号反向。^[2]

几何的直观解释：如果一个函数f(x)在某个区间I上有f''(x)（即二阶导数）>0恒成立，那么在区间I上f(x)的图象上的任意两点连出的一条线段，这两点之间的函数图象都在该线段的下方，反之在该线段的上方。

（2）判断函数极大值以及极小值。

结合一阶、二阶导数可以求函数的极值。当一阶导数等于0，而二阶导数大于0时，为极小值点。当一阶导数等于0，而二阶导数小于0时，为极大值点；当一阶导数和二阶导数都等于0时，为驻点。

（3）函数凹凸性。

设f(x)在[a,b]上连续，在（a,b)内具有一阶和二阶导数，那么，

（1）若在（a,b)内f''(x)>0,则f(x)在[a,b]上的图形是凹的；

（2）若在（a,b)内f’‘(x)<0,则f(x)在[a,b]上的图形是凸的。