- 晶体x射线衍射

晶体x射线衍射
详解名词
X-ray diffrection by crystals X射线在晶体中发生的衍射现象。晶体具有点阵结构,点阵结构的周期(即晶胞边长,b,c)与X射线的波长属于同一数量级,X射线衍射现象是一种基于波叠加原理的干涉现象,干涉的结果随不同而有所不同(Δ为波程差;λ为波长)。为整数的方向,波的振幅得到最大程度的加强,称为衍射,对应的方 向为衍射方向 ,而为半整数的方向,波的振幅得到最大程度的抵消。因此,X射线通过晶体之后,在某些方向(衍射方向)X射线的强度增强,而另一些方向X射线强度却减弱甚至消失 ,如果在晶体的背后放置一张感光底片,将会得到X射线的衍射图形。
晶格参数或晶胞的大小和形状
利用X射线衍射原理制造的X射线衍射仪,是测定晶体结构的最主要仪器。根据衍射的方向可以测定晶格参数或晶胞的大小和形状。根据衍射线强度分布能够测定原子在晶胞中的坐标,因此X射线衍射法也是测定分子空间构型的主要方法。 产生晶体X射线衍射的条件可用劳厄方程来描述,劳厄方程的标量表达式如下: (cos-cos0)=hλ b(cosβ-cosβ0)=kλ c(cosγ-cosγ0)=lλ式中、b、c为晶胞边长;0、β0、γ0是入射线与晶胞基向量的夹角;、β、γ是衍射线与晶胞基向量的夹角;h、k、l是三个正整数,称为衍射指数;λ是X射线的波长。
布拉格方程
描述X射线衍射条件,还可以用布拉格方程: 2dsinθ=nλ式中d为相邻两个晶面之间的距离;θ为入射线或反射线与晶面的交角;λ为X射线波长;n为正整数。布拉格方程与劳厄方程虽然表达方式不同,但其实质是相同的。 当 X射线的波长与入射线方向以及晶体方位确定以后,劳厄方程中的λ、、b、c、0、β0、γ0 都已确定,只有、β、γ是变量,它们必须满足劳厄方程,但是,、β、γ3个变量不是独立的,例如在直角坐标中应满足: cos2+cos2β+cos2γ=1这就是说,3个变量、β、γ应同时满足4个方程,这在一般条件下是不可能的,因而得不到衍射图。为了解决这个问题,必须再增加一个变数,有两种办法可供选择:①晶体不动(0、β0、γ0固定),改变波长λ,即采用白色X射线,这种方法称为劳厄法;②波长不变,即用单色X射线 ,让晶体绕某晶轴转动,即改变0、β0、γ0 。这样可在某些特定的晶体方位得到衍射图,这种方法叫做转动晶体法。以上两种方法都是对单晶体而言的。如果晶体是多晶,每个小单晶体在空间的取向是随机的,劳厄方程总可以得到满足,这就是粉末法的基础。
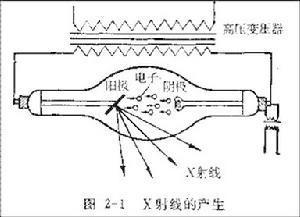 X射线衍射的基本原理
X射线衍射的基本原理
简史

-
哈弗F7/F7x携手汪涵将超值钜惠进行到底 欢迎品鉴
2025-09-20 20:30:48 查看详情 -
江淮嘉悦X7正式上市 售5.97万元起/续航201km
2025-09-20 20:30:48 查看详情 -
捷途X95热爱Pro版上市 别克微蓝6插混车型上市
2025-09-20 20:30:48 查看详情 -
捷途X95热爱Pro版上市 补贴后售19.98万元起
2025-09-20 20:30:48 查看详情 -
有望在5月底上市 全新宝马X5
2025-09-20 20:30:48 查看详情 -
PRO上市 SWM斯威X7冠军版将于5月31日上市
2025-09-20 20:30:48 查看详情 -
一汽丰田bZ4X正式上市 成都车展:奇瑞瑞虎5x西南区域上市
2025-09-20 20:30:48 查看详情 -
首付15800就能贷SWM斯威X7回家过年 油电混合
2025-09-20 20:30:48 查看详情 -
将于2月28日正式上市 东风标致408X正式下线
2025-09-20 20:30:48 查看详情 -
4月16日上市 东风标致408X将于2月16日下线
2025-09-20 20:30:48 查看详情


 求购
求购

