- 圆的一般方程

圆的一般方程
简介
圆是最常见的、最简单的一种二次曲线。
定义
在平面上到一定点(中心)有同一距离(半径)之点的轨迹叫做圆周,简称圆。
标准方程
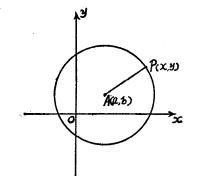
圆半径的长度定出圆周的大小,圆心的位置确定圆在平面上的位置。如果已知:(1)圆半径长R;(2)中心A的坐标(a,b),则圆的大小及其在平面上关于坐标轴的位置就已确定(如右图)。根据图形的几何尺寸与坐标的联系可以得出圆的标准方程。结论如下:
![]() 当圆的中心A与原点重合时,即原点为中心时,即a=b=0,圆的方程为:
当圆的中心A与原点重合时,即原点为中心时,即a=b=0,圆的方程为:
![]()
圆的一般方程
圆的标准方程是一个关于x和y的二次方程,将它展开并按x、y的降幂排列,得:
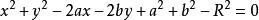
设D=-2a,E=-2b,F=a2+b2-R2;则方程变成:
![]()
任意一个圆的方程都可写成上述形式。把它和下述的一般形式的二元二次方程比较,可以看出它有这样的特点:(1)x2项和y2项的系数相等且不为0(在这里为1);(2)没有xy的乘积项。[2]
![]()
推导过程
由圆的标准方程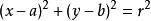 的左边展开,整理得
的左边展开,整理得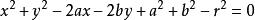 ,在这个方程中,如果令
,在这个方程中,如果令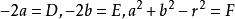 ,则这个方程可以表示成
,则这个方程可以表示成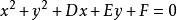 。
。
推论
可以证明,形如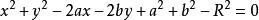 一般表示一个圆。
一般表示一个圆。
为此,将一般方程配方,得:
![]() 为此与标准方程比较,可断定:
为此与标准方程比较,可断定:
(1)当D2+E2-4F>0时,一般方程表示一个以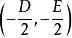 为圆心,
为圆心,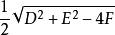 为半径的圆。
为半径的圆。
(2)当D2+E2-4F=0时,一般方程仅表示一个点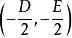 ,叫做点圆(半径为零的圆)。
,叫做点圆(半径为零的圆)。
(3)当D2+E2-4F<0肘,没有一个点的坐标满足圆的一般方程,即一般方程不表示任何图形,叫做虚圆。
圆的标准方程的优点在于它明确地指出了圆心和半径,而一般方程突出了方程式上的特点,便于区分曲线的形状。[2]
举例
求方程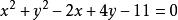 的轨迹。
的轨迹。
解:这个方程的x2和y2项的系数都是1,并且没有xy项,它与圆的方程有相同的形式.我们把它配方,得:
即:
![]()
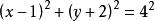
由此可知,原方程的轨迹是一个以点(1,-2)为圆心,4为半径的圆。[3]

-
非线性方程组数值解法
2025-09-19 21:23:59 查看详情 -
奥迪一般几年开始烧机油
2025-09-19 21:23:59 查看详情 -
奥迪a4发动机故障灯亮了一般是什么情况
2025-09-19 21:23:59 查看详情 -
摩托用什么机油(摩托车一般用什么机油)
2025-09-19 21:23:59 查看详情 -
大众加几号油(大众一般加几号油)
2025-09-19 21:23:59 查看详情 -
F1方程赛车逆向设计
2025-09-19 21:23:59 查看详情 -
三款小排量小型SUV雪铁龙C3 1.8L车型的油耗方程式
2025-09-19 21:23:59 查看详情 -
成都车展:一汽奔腾无限方程架构发布/第三代B70将问世 e
2025-09-19 21:23:59 查看详情 -
雪铁龙C3 1.8L车型的油耗方程式
2025-09-19 21:23:59 查看详情


 求购
求购




