- 逆矩阵

逆矩阵
定义
一个n阶方阵A称为可逆的,或非奇异的,如果存在一个n阶方阵B,使得
![]() 则称B是A的一个逆矩阵。A的逆矩阵记作A-1。
则称B是A的一个逆矩阵。A的逆矩阵记作A-1。
定理
(1)验证两个矩阵互为逆矩阵
![]()
按照矩阵的乘法满足: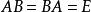 故A,B互为逆矩阵。
故A,B互为逆矩阵。
(2)逆矩阵的唯一性
若矩阵A是可逆的,则A的逆矩阵是唯一的。
证明:
若B,C都是A的逆矩阵,则有
![]() 所以B=C,即A的逆矩阵是唯一的。
所以B=C,即A的逆矩阵是唯一的。
(3)判定简单的矩阵不可逆
如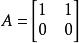 。假设有
。假设有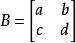 是A的逆矩阵,则有
是A的逆矩阵,则有
![]()
比较其右下方一项:0≠1。[1]
若矩阵A可逆,则 |A|≠0
若A可逆,即有A-1,使得AA-1=E,故|A|·|A-1|=|E|=1
则|A|≠0
性质
性质定理
- 可逆矩阵一定是方阵。
- 如果矩阵A是可逆的,其逆矩阵是唯一的。
- A的逆矩阵的逆矩阵还是A。记作(A-1)-1=A。
- 可逆矩阵A的转置矩阵AT也可逆,并且(AT)-1=(A-1)T(转置的逆等于逆的转置)
- 若矩阵A可逆,则矩阵A满足消去律。即AB=O(或BA=O),则B=O,AB=AC(或BA=CA),则B=C。
- 两个可逆矩阵的乘积依然可逆。
- 矩阵可逆当且仅当它是满秩矩阵。
证明
- 逆矩阵是对方阵定义的,因此逆矩阵一定是方阵。设B与C都为A的逆矩阵,则有B=C
- 假设B和C均是A的逆矩阵,B=BI=B(AC)=(BA)C=IC=C,因此某矩阵的任意两个逆矩阵相等。
- 由逆矩阵的唯一性,A-1的逆矩阵可写作(A-1)-1和A,因此相等。
- 矩阵A可逆,有AA-1=I 。(A-1)TAT=(AA-1)T=IT=I ,AT(A-1)T=(A-1A)T=IT=I由可逆矩阵的定义可知,AT可逆,其逆矩阵为(A-1)T。而(AT)-1也是AT的逆矩阵,由逆矩阵的唯一性,因此(AT)-1=(A-1)T。
- 1)在AB=O两端同时左乘A-1(BA=O同理可证),得A-1(AB)=A-1O=O而B=IB=(AA-1)B=A-1(AB),故B=O2)由AB=AC(BA=CA同理可证),AB-AC=A(B-C)=O,等式两边同左乘A-1,因A可逆AA-1=I 。得B-C=O,即B=C。
可逆等价条件
若|A|≠0,则矩阵A可逆,且
![]()
其中,A*为矩阵A的伴随矩阵。
证明:
必要性:当矩阵A可逆,则有AA-1=I 。(其中I是单位矩阵)
两边取行列式,det(AA-1)=det(I)=1。
由行列式的性质:det(AA-1)=det(A)det(A-1)=1
则det(A)≠0,(若等于0则上式等于0)
充分性:有伴随矩阵的定理,有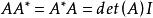 (其中
(其中![]() 是的伴随矩阵。)
是的伴随矩阵。)
当det(A)≠0,等式同除以det(A),变成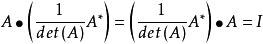
比较逆矩阵的定义式,可知逆矩阵存在且逆矩阵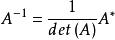
逆矩阵求法
求逆矩阵的初等变换法
将一n阶可逆矩阵A和n阶单位矩阵I写成一个nX2n的矩阵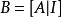 对B施行初等行变换,即对A与I进行完全相同的若干初等行变换,目标是把A化为单位矩阵。当A化为单位矩阵I的同时,B的右一半矩阵同时化为了A的逆矩阵。
对B施行初等行变换,即对A与I进行完全相同的若干初等行变换,目标是把A化为单位矩阵。当A化为单位矩阵I的同时,B的右一半矩阵同时化为了A的逆矩阵。
如求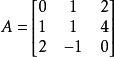 的逆矩阵A-1。
的逆矩阵A-1。
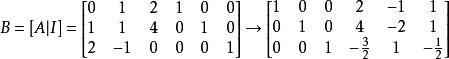
故A可逆并且,由右一半可得逆矩阵A-1=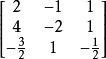
初等变换法计算原理
若n阶方阵A可逆,即A行等价I,即存在初等矩阵P1,P2,...,Pk使得
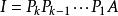 ,在此式子两端同时右乘A-1得:
,在此式子两端同时右乘A-1得: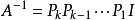
比较两式可知:对A和I施行完全相同的若干初等行变换,在这些初等行变化把A变成单位矩阵的同时,这些初等行变换也将单位矩阵化为A-1。[2]
如果矩阵A和B互逆,则AB=BA=I。由条件AB=BA以及矩阵乘法的定义可知,矩阵A和B都是方阵。再由条件AB=I以及定理“两个矩阵的乘积的行列式等于这两个矩阵的行列式的乘积”可知,这两个矩阵的行列式都不为0。也就是说,这两个矩阵的秩等于它们的级数(或称为阶,也就是说,A与B都是方阵,且rank(A) = rank(B) = n)。换句话说,这两个矩阵可以只经由初等行变换,或者只经由初等列变换,变为单位矩阵[3]。
伴随矩阵法
如果矩阵![]() 可逆,则
可逆,则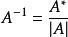
注意:![]() 中元素的排列特点是的第k列元素是A的第k行元素的代数余子式。要求得
中元素的排列特点是的第k列元素是A的第k行元素的代数余子式。要求得![]() 即为求解
即为求解![]() 的余因子矩阵的转置矩阵。A的伴随矩阵为
的余因子矩阵的转置矩阵。A的伴随矩阵为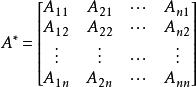 ,其中Aij=(-1)i+jMij称为aij的代数余子式。
,其中Aij=(-1)i+jMij称为aij的代数余子式。



 求购
求购










