玻色-爱因斯坦冷凝物

那为什么冠以玻色－爱因斯坦的名字呢？有这样一 段插曲。 　1924年，年轻的印度物理学家玻色寄给爱因斯坦一篇论文，提出 了一种新的统计理论，它与传统的统计理论仅在一条基本假定上不同。 传统统计理论假定一个体系中所有的原子（或分子）都是可以辨别的， 我们可以给一个原子取名张三，另一个取名李四……，并且不会将张 三认成李四，也不会将李四认成张三。基于这一假定的传统理论圆满 地解释了理想气体定律，可以说取得了非凡的成功。然而玻色却挑战 了上面的假定，认为在原子尺度上我们根本不可能区分两个同类原子 （如两个氧原子）有什么不同。接着，玻色讨论了如下一个问题（这 个问题所有高中生都做过）：将N个相同的小球放进M个标号为1,2,…, M的箱子中，假定箱子的容积足够大，有多少种不同的放法？在此问 题的基础上，采用传统统计相似的作法，玻色便得到了一套新的统计 理论。 玻色的论文引起了爱因斯坦的高度重视，迅速帮玻色译成德文发表。随后将玻色的理论用于原子气体中，进而推测在足够低的温度下， 所有原子有可能处在相同的最低能态上，所有的原子的行为像一个粒子一样。后来物理界将这种现象称为玻色－爱因斯坦凝聚。值得注意的是，这里的“凝聚”与日常生活中的凝聚不同，它表示原来不同状 态的原子突然“凝聚”到同一状态。

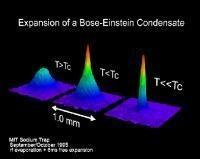
爱因斯坦的预测引起了实验物理学家的广泛兴趣。然而实现BEC的条件极为苛刻和“矛盾”：一方面希望达到极低的温度，另一方面 还要求原子体系处于气态。实现低温的传统手段是蒸发制冷；而朱棣文、Cohen-Tannoudj和Phillips发展的激光冷却和磁阱技术是另一种有效 的制冷方法，他们三人因此分享了1997年度诺贝尔物理学奖。1976年， Nosanow和Stwalley证明在任意低温下处于自旋极化的氢原子始终能保持气态，则为实现第二个要求提供了希望。 　但遗憾的是，众多的实验物理学家将自旋极化的氢原子气体降温，并未观察到BEC现象。于是Wieman和Cornell开始将兴趣转向碱金属原子气体，1995年，他们将铷原子限制在磁阱中进行激光冷却首次成功的观察到原子气的BEC现象。同年，MIT的Ketterle也在钠原子气中实现了BEC。BEC的实现不仅在基础研究方面具有重大意义，还可能在 “原子芯片”和量子计算机等方面有广泛的应用前景。因此诺贝尔l物理学奖授予Wieman、Cornell和Ketterle以表彰他们在BEC实验 方面的开创性工作。

Ketterle在纳原子气中实现的BEC，从实现BEC的历程来看，有以下两个必备的客观条件：首先是理 论准备（玻色和爱因斯坦的工作），其次是实验手段的进步（朱棣文 等人的工作）。剩下的就是个人的素质了，要有眼光，走对路（Wieman、 Cornell和Ketterle选择碱金属原子气体作为冷却的对象）。这样看来， 诺贝尔物理学奖似乎不是什么神秘的东西。因此有人就会问为什么中 国内地就没有出现诺贝尔奖呢？下面谈谈我的个人看法。诺贝尔物理学奖的宗旨是：“奖给在物理学领域内作出最重要的 发现或发明的人”。从这一宗旨来看，目前内地的实验条件远远达不到产生诺贝尔（实验）奖项的条件，在理论工作领域出现突破可能相对容易一些，但这些突破必须是重大的原始创新，它实质上是科学气氛于科学精神的产物，以下条件是必不可少的：

1、思想开放，不迷信权威。创新就是要打破某些已有的定论，因循 守旧，盲从权威是不可能有所创新的。中国的知识分子经历了太多的 苦难以及封建思想的残余，以至于思想里保守成分多，权威意识过强， 传统教育中以循规蹈矩为优等等都不利于创新。

2、科学文化的沉淀。任何重大创新不是凭空冒出来的，创新必须以 继承已有的优秀科学成果和思想方法为前提，这种科学文化需要长时 间的积累。而中国内地真正科学文化的萌芽起于1919年的五四运动， 后来又受文革的严重冲击，因此真正的科学文化沉淀也就20来年时间， 比起西方三四百年简直是小菜。热情奔放而又执著追求科学的年轻人。据中科院2001年科学发展报告统计，诺贝尔物理学奖得主作出代表性工作的平均年龄为36岁，他们从很小就开始对物理学感兴趣并一直钟爱着物理学。他们能如此 执著，一方面是经济条件还不错，更重要的是他们从小所受的教育是以充分发挥自己的个性为主。而内地的教育更乐意将学生培养成标准 的螺丝钉，学生本人则很少有太多的想法和目标，在经济大潮的影响 下立刻便沉到“海”里去了。

总之，诺贝尔物理学奖是在继承前人优秀的成果基础上的重大创 新，目前中国内地并不具备上述创新的条件。但值得庆幸的是，自改 革开放以来，思想界也有所解放，国家对科学重视程度提高，国际交 流与合作也日益广泛和深入，我想经过漫长时间的努力，中国大陆有望出现诺贝尔物理学奖。

对于波色子，粒子满足对易关系，同一个量子态（能级）的粒子数占据可以是无穷大。

在高温，不同能级的粒子占据数满足波色分布，在热力学极限下，每个能级的粒子数都是微观小量（相比于宏观量总粒子数）。
随着温度降低，粒子倾向于占据能量更低的态来降低体系的能量（体系总是处在自由能最低的态，自由能包含能量和熵，这两者竞争，能量要求体系尽可能占据低能级的态，熵要求体系尽可能占据更多不同的能级，高温时熵要求占主导地位，低温时能量要求占主导地位），所以越来越多的粒子占据最低能级，在临界温度下，有宏观量的粒子数（相比于宏观量总粒子数）占据最低能级，这样最低能级的这些粒子全体形成一个宏观相干量子态，体系发生波色爱因斯坦凝聚。
对于具有平移不变性的体系，动量是一个好量子数，体系的能级可以用动量来标志，比如最低能量的能级对应动量为零的态，所以我们一般说波色爱因斯坦凝聚是发生在动量空间。
理论上，无相互作用的波色气体就可以发生波色爱因斯坦凝聚，但是如果过渡到经典极限，我们会发现波色子的对易关系可以等效地认为粒子间有吸引相互作用，所以这个无相互作用的波色气体是量子力学意义下的（对应地，费米子的反对易关系可以等效地认为粒子间有排斥相互作用，根据泡利不相容原理，同一个量子态只能被一个费米子占据）
但是实际上波色体系间总是有相互作用的，如液氦4，吸引和排斥相互作用如何对波色爱因斯坦凝聚临界温度的影响（也就是促进还是削弱凝聚的发生），有待补充。
对于相互作用波色体系发生波色爱因斯坦凝聚，体系会形成超流态，如低温的液氦4。

对于费米系统，由于泡利不相容原理，即使在零温，也不能发生凝聚，即同一个能级有宏观数目的粒子占据数。但是如果费米子之间有吸引相互作用，两个费米子形成一个束缚态。两个费米子组成的复合粒子是波色子，对于这些波色子（在超导里我们一般称为库伯对），根据之前讨论的波色爱因斯坦凝聚，这些库伯对可以在低温下发生波色爱因斯坦凝聚。

波色爱因斯坦凝聚称为BEC
常规超导理论称为BCS（可以认为费米子的凝聚）
把这两个概念同时考虑，就是冷原子里现在大家在玩的BCS-BEC crossover

超流反应了体系密度密度关联性质，超流里面的氦原子是中性原子，发生BEC时有U（1）对称性的自发破却，所以有无能隙的Goldstone模
超导反应了体系流流关联性质，超导里面的电子还有电荷，必须考虑电磁场和BEC的耦合，根据Anderson-Higgs机制，电磁场会吃掉Goldstone模，所以超导会有能隙。

对于费米系统凝聚（例如超导，He3超流，以及某些冷原子系统）来说，BCS和BEC只是两个极限情况。两者破坏的都是U(1) symmetry。

费米系统凝聚一般来说存在两个能标（或者说温度），一个是两个费米子配对，形成Cooper pair，或者说是一个bound state，我们管这个温度叫Tb。另一个是Cooper pair形成global phase coherence，我们管这个温度叫Tc。BCS对应的极限是Tb=Tc，也就是有了Cooper配对，就有了phase coherence，出现超导、超流等现象。传统的金属超导都在BCS极限。BEC对应的极限是Tc<<Tb。也就是费米子首先配对，形成波色系统。但在这个时候，系统并没有进入超导相，反而，由于Cooper对能隙的出现，系统其实是insulator。直到温度降到Tc，系统才出现超导。一般来说，对于冷原子系统，由于原子密度很低，费米能很小，以至于和Cooper pair的bound energy处于同一个energy scale，因而都处于BEC极限。而在两个极限之间的情况，称作BCS-BEC crossover。

在日常生活中我们所感受到的物质世界是由质子、中子、电子和光子组成的。其中前三者自旋量子数均为s=1/2，它们被称为费米子；光子的量子数是整数s=1，被称为玻色子，它是电磁相互作用的媒介粒子。

对于原子来说，它究竟属于费米子还是玻色子，需看构成原子的费米子(质子、中子和电子)的总数。He，Li，K中的费米子总数分别为5，9和59，因而是费米原子；H，He，Li，Na，Rb和Cs中的费米子总数分别为2，6，10，34，124和188，因而是玻色原子[1]。1925年，在玻色理论工作的基础上，爱因斯坦预言了一种新的低温物质形式：气态玻色子系统，在某一临界温度以下，将有宏观数量的粒子共同占据量子力学基态——后来被叫作BEC。

事实上，对于BEC现象的观察要早于爱因斯坦的预言。1911年发现的超导现象(金属汞)就是一种BEC。超导发生在电子(费米子)系统，要使电子凝聚到单一量子态，首先要求电子配对——形成自旋量子数为整数(而不是半整数)的“库柏对”。在超导体中所发生的正是作为玻色子的库柏对的凝聚。1938年发现的液He超流也属于BEC现象。在临界度T_C=2.17K以下，与超导中无阻的电流现象相类似，超流He在毛细管中的流动不显示任何粘滞。与He原子不同，He属于费米原子，因此在He原子配对之前，液He不可能超流。He的超流转变温度很低(～2mK)，因此直到1972年才观察到He超流现象。

1995年，在中性碱金属原子气系统中产生BEC的实验取得了成功，它是建立在“激光冷却和捕获原子”的技术基础之上的[2]。这类BEC与前面所说的超导、超流现象有所不同，后二者的凝聚发生在动量空间，而前者发生在位置空间。在本文的以下部分，BEC术语专指碱金属原子气在三维位置空间所发生的凝聚。在一般情况下，金属蒸气在冷却时会凝结成液体，进而转变成固体。在固体中原子活动的范围相对固定，其中的原子不可能凝聚到位置空间的单一量子态。与固体中的情况相反，碱金属(Li，Na，Rb)蒸气可经激光冷却而快速降温(成为过冷蒸气)，以至于在它们还没来得及凝固成块以前，经彼此之间的频繁碰撞取得共同的能量状态[2]。

第一批实现BEC(1995年)的几个研究小组分别来自美国科罗拉多实验室天体物理联合研究所(简称JILA)(E.Cornell和C.Wieman)；美国麻省理工学院(MIT)(W.ketterler等)；美国莱斯大学(R.Hulet等)[2]。此后，有关BEC的研究发展迅速。1997年BEC中的相干性获得了验证[3]。接着，观察到了一系列新现象，如BEC中的约瑟夫森效应[4,5]，涡旋[6,7]和超冷费米原子气等[8,9]，其中有些现象是玻色和爱因斯坦当年所未曾想象过的。于是，BEC召致了诸多领域现代物理学家的关注。

对于BEC怀有满腔热忱的包括一批天文物理学家——他们甚至希望以BEC为模型，研究宇宙中天体之间的相互作用，进而探索宇宙大爆炸初期的时空结构[10,11]。

二、BEC的产生

下面介绍JILA用Rb蒸气产生BEC的实验[2]。在实施激光冷却之前，Rb蒸气被引入一个真空的玻璃小盒。盒外绕有特殊构形的电流线圈，用于产生静态或动态的磁场。六束激光从上下、左右、前后六个方向射向玻璃盒。激光的频率被调整到略小于原子从能级5s_1/2跃迁到5p_3/2所需的频率。玻璃盒中的原子运动是杂乱无章的，包含着指向空间任何方向的运动。考虑一个向右运动的Rb原子，它将会与一个从右方射来的光子相碰。由于多普勒效应，在这个原子看来，激光的频率略有增高，以至于光子能量正好等于它跃迁到较高能态所需的能量。原子在吸收这个光子之后，原来向右的动量减小了。此后，该原子会通过自发发射光子而回到低能态，但这种发射在方向上是随机的，对增加特定方向的动量没有贡献。玻璃盒中的每一个Rb原子都将经历上述动量幅值减小的多普勒过程，加上一些其他随伴的冷却机制(如偏振梯度冷却)，蒸气原子系统的整体温度(平均动能)在一分钟内就可以被降至T～40μK。与此同时，在激光束辐射压力和弱磁场的共同作用下，蒸气原子聚集到玻璃盒的中央，从而避免了与室温环境的热交换。

无论是费米原子还是玻色原子，它们的原子核均具有微小的核磁矩。核磁矩是μ_I量级，这仅仅是电子磁矩(μ_B量级)的大约千分之一。核磁矩与价电子磁矩的相互作用，将导致碱金属原子的基态(2s_1/2)能级一分为二——形成所谓基态超精细结构。H原子的核自旋量子数是1/2，它的超精细结构量子数为F1=0和F2=1。Li，Na，Rb原子的核自旋均为3/2，它们的超精细上下能级分别是F1=1和F2=2。对于Rb，二个超精细能级之差，ΔE=hν_HFS=h×6834MHz =k_BT=k_B×0.328K，其中h代表普朗克常数。

经激光冷却后，Rb原子蒸气的温度仍比BEC转变临界温度(170nK)高出200多倍。接下来的工作是对其实施蒸发冷却。在磁场的作用下超精结构F1和F2能级会进一步发生塞曼分裂：F1=1分裂为m_F=0,±1；F2=2分裂为m_F=0，±1，±2。处于不同塞曼支能级的原子磁矩相对于外磁场的取向也不同。其中顺应磁场方向的，在磁场梯度力的作用下被约束到玻璃盒的中央，而相反方向的原子磁矩则不受约束。如果用射频脉冲照射预冷后的原子云，将会打乱原子矩的取向，使大部分原子矩脱离磁场约束。这其中速度较高(动量较大)者将有时间，在磁场重新捕获它们之前从磁势阱中逃逸，即通过蒸发带走原子云中的内能。剩下来的原子平均动能较低，依靠彼此之间的频繁碰撞，原子云的整体温度进一步降低，最终产生BEC。

目前所能获得的BEC，其原子数不是很大，只有大约10个原子。如果按照经典物理把凝聚体视为密堆的刚球，看上去，它的总尺寸仅数十nm。JILA的实验者对BEC的成象表明，原子云的尺寸相当于经典图象的上千倍。在BEC原子云中，每个原子以剩余的量子力学零点能缓慢地运动着——动量Δp很小。由于不确定关系，Δx·Δp≈?(?=h/2π)，它们在位置空间的活动范围便较大。作为凝聚到单一量子态的一个整体，此时原子间的平均距离小于原子的德布罗意波长(λ_d)。

三、原子钟

1995年，在第一次实现Rb的BEC之后，人们首先想到的应用是改进现有的原子钟。在1956—1964年，时间的标准是通过地球绕太阳运行的公转周期定义的：一秒等于一年时间的31556925.9747分之一。为复现这一标准，需作长期烦琐的天文观察，并且精度只能达到1/10。随着原子光谱技术的发展，人们开始利用原子超精细结构的本征性质作为守时基准。1964年，国际计量委员会通过议案，以Cs原子基态(6s_1/2)的超精细能级差来定义秒：1s=9192631770×(1/ν_铯)，其中ν_铯是激发F1=3到F2=4共振跃迁的微波频率。也就是说，上述电磁振荡大约92亿个周期所持续的时间被规定为一秒。今天，计量用原子钟的守时精度已经达到了1/10的水平。换句话说，每30万年才会产生一秒的误差。

铯原子钟主要由谐振腔，微波馈入机构和频率可调的晶体振荡器组成。处于超精细低能态(F1=3)的铯原子蒸气被送入谐振腔。如果馈入的微波频率接近ν_铯，则腔中原子就会产生从F1=3到F2=4的感应跃迁。通过检测跃迁原子的比例，可以辨认是否实现共振。微调晶体振荡器频率，当最大跃迁出现，此时的微波频率即等于ν_铯。将该频率的振荡信号送入电子计数器，每当计数器读出9192631770个周期，就意味着时间又度过了一秒。目前，各国计量部门使用的铯原子蒸气，已经是经过了激光冷却的。如果铯原子蒸气直接取自BEC，共振跃迁的信号将更为尖锐，时间的计量精度有望再提高100倍——优于1/10。

四、原子激光

如果以某种方式令原子从BEC中射出，原子束将表现出极佳的波动相干性，产生所谓“原子波激射”，俗称“原子激光”。将一团BEC原子云劈成两半，然后令它们在重力场中下落。每一半在下落过程中均自由膨胀，并且逐步发展彼此的重叠。此时，通过吸收成象，可以在交叠区观察到明暗相间的条纹。1997年Ketterler等首先完成了这样的实验(对Na蒸气)，测得的条纹间距是～15μm[3]。这意味着，作为物质波输出的Na原子束，其德布罗意波长λ_d～30μm。利用量子力学关系v=h / mλ_d(m是Na原子质量)，可以得到Na原子在水平方向的扩展速度，v≈0.6mm/s。这一速度仅为室温下速度的3/10。

相干原子束与普通激光的根本区别在于，它的干涉条纹反映了实物原子的密度分布。用参考激光束照射一张激光全息底片，我们可在底片的另一侧观察到拍摄目标的立体实象。如果将全息技术用于BEC相干原子束，所得到的将不仅仅是立体实象，而是实实在在的三维客体。预计，通过原子全息技术可以精确地定位原子，制造纳米集成电路或改造纳米生物体。不过，近期还不能指望用原子激光制造pc计算机的芯片，因为所能得到的BEC量实在是太少了——只有大约1/10克。

严格地说，Ketterler小组的相干原子团不是从BEC中射出而是“滴出”的，它只能算是物质波激射的雏形。为了使相干原子束更象激光，德国马普光学所的T.Hansch小组[12]、美国耶鲁大学的M.Kasevich等[13]和美国国家标准技术研究院(NIST)的W.Phillips小组[14]相继作出了重要的技术进展。Kasevich等的BEC输出也是向下滴出的，但原子云滴的尺寸不再随时间而胀大。Hansch小组解决了云滴不连续的问题，原子波束也很少发散，但与前二者一样也是在重力的驱动下向下发射。

1999年，Phillips小组使用相干受激拉曼耦合输出技术，大大减小了发射原子束的扩展，获得了准直性极佳的(发散角仅为0.1°)原子激光；更重要的是，相干原子束的发射可以按照需要指向空间的任何方向[14,15]。Phillips小组的作法是，在Na - BEC形成之后，令磁势阱的尺寸突然膨胀，从而使BEC原子的活动范围Δx增大，而动量分布的宽度Δp减小。用一对频率接近但方向大致相反的激光以脉冲的方式照射凝聚体。BEC原子先吸收正方向的光子?ω₁，跃迁到能量较高的塞曼支能级，然后该原子在负方向激光脉冲的作用下受激发射?ω₂光子返回到原先的塞曼支能级。经上述双光子过程，BEC原子的磁能没有变化，但却获得了正方向的动量，mv=2h/λ，其中λ=589nm是引发拉曼散射的激光波长。计算和实验均表明，Na原子沿发射方向的飞行速度v≈6cm/s，从而使得定向相干原子束成为准连续的。

五、约瑟夫森效应

相干物质波物理与超导、超流物理具有共同的范式(paradigm)——约瑟夫森效应。范式的核心概念是：在宏观量子系统中物理量也将展示出位相相干关系。

以极薄的绝缘层分隔两块超导体、即可制成弱连接的约瑟夫森结。如果在结的两边加直流电压V，一个圆频率ω_J= 2eV/?(e是电子电荷)的交变电流将会在结中产生。这就是所谓交流约瑟夫森效应。对于计量工作来说，实现频率的高精度测量要比直流电压测量容易得多，因此各国计量部门都以上述关系构建电压基准[16]。

1998年，Kasevich小组通过激光驻波场在Rb原子BEC中构成了约瑟夫森结[4,5]。驻波场沿重力方向分布，毗邻波节间的距离等于激光波长λ的一半。在驻波场中，BEC原子将聚集到各个波腹位置，因为在这些位置能够得到更有效的冷却，结果，BEC原子的空间分布形成了一维“光学晶格”，也即一串竖直分布的约瑟夫森结。毗邻约瑟夫森结之间的重力势能差ΔU_G= mgλ/2 (g是重力加速度)与超导结中的化学势差Δμ=2eV相对应。于是，当光学晶格中的BEC原子在重力场中下落，在原子流中将会含有圆频率为ω_J= mgλ/2?的交流成份。

对下落的原子流摄取闪光快照，所呈现的正如一个钢球在重力场中自由下落的等时差多次闪光照片(在高中物理课本中有此照片)。从下落原子流滴之间的空间间隔，可以反演出交流成份的周期，其实验值是1.10±0.05ms；而与g= 9.8m/s相应的理论周期是1.09ms，二者相符很好。随着实验技术的进一步改进，或许有一天，人们可以利用BEC中的等效约瑟夫森效应，更加精确地测量重力加速度g。

六、BEC中Rb二聚物分子的形成

在原子BEC的基础上生产出二聚物分子BEC，在理论和实验两方面均具有重要意义。最近，制备Rb₂分子BEC的实验已在美国德克萨斯大学获得了成功[17,18]。实验者们使用固定频差(ν₂-ν₁= 636MHz )的二束同方向激光以拉曼脉冲的方式照射Rb原子云。第一束脉冲将一对Rb原子激发至高能二聚态(二个Rb原子束缚成对)，然后第二束脉冲诱发束缚对从高能二聚态受激发射，使束缚对向下跃迁至一个比Rb原子基态能级更低的能态——即Rb₂分子的BEC态。目前的技术只能将部分BEC原子转变成BEC分子。但理论预言，采用拉曼光缔合技术，最终将可能生产出纯的分子BEC。人们设想，如果用二束方向相反的脉冲照射BEC分子云将有可有使BEC分子具有(h/λ₁)+(h/λ₂)的定向动量，从而形成“分子激光”。

七、超冷费米原子气

如前所述，费米原子气不可能实现BEC。那么在超冷条件下，费米原子蒸气将会是什么样子呢?最近，来自JILA的D.S.Jin和她的研究生以独具匠心的技术路线，成功地将100万个K费米原子冷却到了300nK，从而第一次获得了服从费米—狄拉克统计的宏观客体[8,9]。CCD成象显示，超冷K原子云具有类壳层结构，就象是孤立原子中核外电子的壳层结构。

蒸发冷却是实现玻色原子凝聚的关键步骤。然而，对于费米原子来说，蒸发冷却很难实现：由于泡利不相容原理的限制，自旋极化的费米原子在位置空间是相互回避的，以至于在高速K原子逃离势阱之后，剩下来的原子难于靠彼此间的碰撞取得更低的平均温度。Jin等采取的对策是：同时捕获二种塞曼支能级略有差异(F=9/2，m_F= 9/2和F=9/2，m_F= 7/2)的K原子。依靠这二类原子彼此的碰撞(m_F= 9/2与m_F= 7/2的碰撞不受泡利原理限制)，恢复蒸发冷却的效率。

在300nK的低温下，与100万个K原子相应的50万个最低能量阶梯中，有60%已被占据。虽然Jin等还未能实现完全的费米简并，但因简并而产生的库仑排斥突增已经清晰地显现出来——超冷K原子云的尺寸不再进一步地缩小。这一现象与中子星平衡重力坍缩具有全同的机理。下一步的工作将指向一个更为神奇的物质态——在更低的温度下，实现费米原子的相互配对，形成类似于超导库柏对的复合玻色原子。

八、BEC中的涡旋

令一只装有水的圆桶绕其对称轴旋转，桶中的水将因桶壁的拖拽随桶一起转动。早年，牛顿曾以经典力学说明了旋转时水面所呈现的抛物面形状。旋转中，越是靠近桶壁的地方，水微团的转动线速度越大[19]。

当我们拔启卫生间水池漏孔的塞子，池中的水将以旋转的方式从漏孔流走，形成所谓“涡旋”。与牛顿转桶的情况相反，在涡旋中，越是靠近中心的地方，流速越大，因此，在涡旋的中央位置必须是空的，否则那里的速度将趋于无穷大[19]。

在宇宙中有许多涡旋星系(我们的银河系就是其中之一)。如果假定星系的大部分质量位于涡旋的中心，那么根据万有引力定律，某一星体轨道运动的速度平方v应正比于1/r(r是星体到轨道中心的距离，即r越大，v越小。然而，天文观测表明，星体的v几乎不随r变化。于是，便引出了“存在暗物质”的假说。

将牛顿转桶中的水换成超流He，由于超流与桶壁之间没有摩擦力，在圆桶转动足够慢的情况下，桶中的超流He将保持静止。当桶的转速逐步增加并超过某一临界角速度，超流He流体中将开始出现涡旋。然而，涡旋在超流He中的存在方式与水中的不同，前者不涉及随容器的整体转动，旋转被限制在一根与转轴平行，直径仅数μm的细丝内——称之为“涡旋芯”。在涡旋芯内，持续流动的环流线速度v_s幅值与环行的半径r成反比，即r越小，v_s越大。当r=0时，则有速度场发散，因此在涡旋芯的中央不应该有流体。

随着超流He容器转速的进一步增加，涡旋芯将一根一根地出现(量子化)。从垂直于液面的方向看去，这些涡旋将排列成规则的点阵结构：3根涡旋排成正三角形，4根排成正方形，7根排成正六边形(其中有一根在六边形的中心)等等。这一现象表明，在同方向旋转的涡旋芯之间存在着排斥相互作用。

涡旋是自然界中的普遍现象，它可以发生在各种尺度和各种介质中。除了上面提到的涡旋星系和超流涡旋外，还有超导体中电子库柏对运动所形成的电流涡旋和宇宙弦等等[1]。对于超流以及BEC这样的单一量子态情况，量子力学波函数的单值性要求：

v_sdl= (?/m)?jdl= nh/m

其中，方程式的左边是流速场v_s沿封闭回路的环流，m是流体原子的质量，?j是波函数位相在空间分布的梯度，n是整数。环流的量子化单位是h/m，而?jdl≡2nπ。

为在BEC中实现涡流观察，关键是要使悬空的BEC原子云转起来。目前有两种办法，其一：用一激光束以特定的圆频率w_r搅动双组分凝聚体(具有不同的塞曼态)，就象用一根筷子搅肉馅。同时，用微波驱动BEC原子在上述二态间上下跃迁，并调控振荡跃迁的有效Rabi频率Ω_eff，使Ω_eff≈ω_r[6,20,21]。其二：令BEC直接在一个转动着的各向异性磁—光阱中产生。用这种办法可以产生多个涡旋，有助于观察转速增加时涡旋点阵排列结构的变化。

最近，法国巴黎高等师范的K.Madison等用上述第二种办法研究了Rb-BEC中涡旋的性质[7]。大约10万个Rb原子在旋转的各向异性势阱中被冷却到80nK以下，在势阱的转动频率从147Hz增加到172Hz的过程中，他们依次观察到了1，2，3，4个量子化涡旋的出现。正如理论所预言的，3根涡旋排成正三角形，4根则排成正方形。在每根涡旋芯的中央，他们也观察到了粒子密度的极小，类似于水从洗脸池漏孔中流出时的中空涡旋。此外，Madison等还收集到了一批有关涡旋形核和涡旋寿命的数据，这将促使有关专家从涡旋元激发的角度深入研究BEC与其超流动性之间的关系。