- 默比乌斯函数

默比乌斯函数
定义
默比乌斯函数或缪比乌斯函数是指以下的函数:
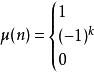 |
若; |
若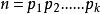 ; ; |
|
| 若 |
μ(n)的首25个值(OEIS中的数列A008683):1, −1, −1, 0, −1, 1, −1, 0, 0, 1, −1, 0, −1, 1, 1, 0, −1, 0, −1, 0, 1, 1, −1, 0, 0, ...
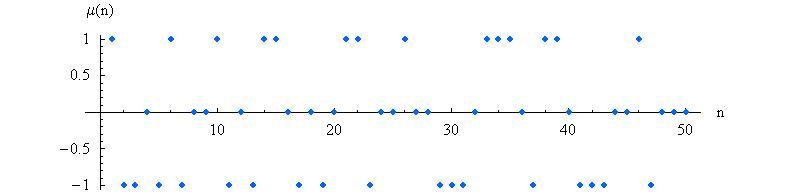 图1.μ的首50个值
图1.μ的首50个值
μ(n) ——默比乌斯函数,关于非平方数的质因子数目。
莫比乌斯函数完整定义的通俗表达:
1)莫比乌斯函数μ(n)的定义域是N;
2)μ(1)=1;
3)当n存在平方因子时,μ(n)=0;
4)当n是素数或奇数个不同素数之积时,μ(n)=-1;
5)当n是偶数个不同素数之积时,μ(n)=1。
性质
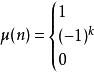 |
若; |
若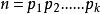 ; ; |
|
| 若 |
性质1
性质2
莫比乌斯函数是一个数论函数,它是一个积性函数。
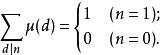
证明:
①当 n=1时显然;
②当n![]() 0时,将n分解可以得到
0时,将n分解可以得到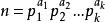 ;
;
在n的所有因子中,![]() 值不为零的只有所有质因子次数都为1的因子,其中质因数个数为r个的因子有
值不为零的只有所有质因子次数都为1的因子,其中质因数个数为r个的因子有![]() 个
个
那么显然有: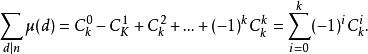
与其他函数的关系
对任意正整数n有:
![]()
证明:
只需要令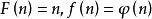 ,代入莫比乌斯反演的公式即可
,代入莫比乌斯反演的公式即可
1.梅滕斯函数
2.生成函数
莫比乌斯函数的求和函数,被称为梅滕斯函数,
![]()
3.无穷级函数
莫比乌斯函数有多个生成函数,其中一个与黎曼的ζ(s)有关:
![]()
相关知识
以下是关于莫比乌斯函数的一些无穷级数:
1)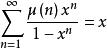
2)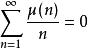
3)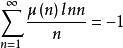

相关百科
-
1641函数信号发生器
2025-09-16 08:47:42 查看详情


 求购
求购










