- 亚纯函数值分布理论
亚纯函数值分布理论
概念
亚纯函数值分布理论是亚纯函数理论中具有深刻而完美理论的一个分支。设w(z)为复平面C上的亚纯函数,令:
 表示圆|z|<r内w(z)的a值点个数(按重级计算),若w(0)≠a,∞,则w(z)的a值点密指量定义为:
表示圆|z|<r内w(z)的a值点个数(按重级计算),若w(0)≠a,∞,则w(z)的a值点密指量定义为:
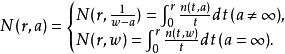 奈望林纳引入特征函数:
奈望林纳引入特征函数:
![]() 其中:
其中:
![]()
![]() 进一步定义w(z)关于a的亏量为:
进一步定义w(z)关于a的亏量为:
![]() 如果δ(a)>0,则称a为亏值。由第二基本定理可得下述重要的亏量关系,即至多有可数多个亏值,且总亏量满足:
如果δ(a)>0,则称a为亏值。由第二基本定理可得下述重要的亏量关系,即至多有可数多个亏值,且总亏量满足:
![]() 近代亚纯函数值分布理论亦称奈望林纳理论,是由芬兰数学家奈望林纳(Nevanlinna,R.)于20世纪20年代创立的。他还建立了两个基本定理且引入新的概念,使得已有的理论或呈现崭新的面貌,或得到重要的推广。亚纯函数奈望林纳理论还被推广于代数体函数、亚纯曲线和多复变亚纯映射等方面,并且成为研究复域常微分方程解析理论的有力工具。
近代亚纯函数值分布理论亦称奈望林纳理论,是由芬兰数学家奈望林纳(Nevanlinna,R.)于20世纪20年代创立的。他还建立了两个基本定理且引入新的概念,使得已有的理论或呈现崭新的面貌,或得到重要的推广。亚纯函数奈望林纳理论还被推广于代数体函数、亚纯曲线和多复变亚纯映射等方面,并且成为研究复域常微分方程解析理论的有力工具。
亚纯函数
除极点外为全纯的函数为亚纯函数,它是复变函数论研究的主要对象之一。
德国数学家外尔斯特拉斯、瑞典数学家米塔-列夫勒、法国数学家柯西等都是亚纯函数理论的奠基人。1876年,外尔斯特拉斯证明了一个亚纯函数可以表示为两个整函数的商。第二年,瑞典数学家米塔-列夫勒推广了外尔斯特拉斯的结果,证明在任意一个区域上的亚纯函数皆可表示为两个函数的商,其中每一个都在该区域内解析。法国数学家柯西也曾给出一种分解方法,对相当广的一类亚纯函数得到简单的表示式。
近代亚纯函数理论是20世纪20年代由芬兰数学家奈望林纳所创立。他在1925年发表了亚纯函数的一个一般性理论,这个理论中有两个基本定理分别被称为第一基本定理和第二基本定理,从它们可以推出一系列关于亚纯函数的值分布的结果,丰富并推进了前人的工作,产生了深远影响。
亚纯函数的术语是由法国数学家布里奥和布凯共同引进的。
代数体函数
代数体函数是亚纯函数或代数函数的推广。设M为亚纯函数域,M[x]表示系数为M的多项式环,则代数体函数域A是M[x]的代数闭包,即任一个w∈A,存在F∈M[x],使得:
![]() 其中Sj(j=0,1,2,…,ν)∈M,或者经通分后w满足下述不可约方程:
其中Sj(j=0,1,2,…,ν)∈M,或者经通分后w满足下述不可约方程:
![]() 其中Aj(z)(j=0,1,…,ν)是z的整函数(通常考虑Aj(z)中至少有一个为超越函数的情形)。特别地,当ν=1时,w(z)为亚纯函数;当Aj(z)(j=0,1,…,ν)都为多项式时,w(z)为代数函数。
其中Aj(z)(j=0,1,…,ν)是z的整函数(通常考虑Aj(z)中至少有一个为超越函数的情形)。特别地,当ν=1时,w(z)为亚纯函数;当Aj(z)(j=0,1,…,ν)都为多项式时,w(z)为代数函数。
代数体函数首先由庞加莱(Poincaré,(J.-)H.)所引入,其后班勒卫(Painlevé,P.)、布特鲁(Boutroux,P.L.)和马尔姆奎斯特(Malmquist,J.)等人研究常微分方程时遇到此类函数。如同亚纯函数一样,代数体函数的主要研究内容之一是它的值分布理论。最早由雷蒙多斯(Rémoundos,G.)(1927)推广了皮卡定理,他证明了ν值代数体函数至多有2ν个皮卡例外值,并指出存在具有2ν个皮卡例外值的代数体函数。其后瓦利隆(Valiron,G.)(1929)、乌利希(Ullricn,E.)(1931)和塞尔贝格(Selberg,A.)(1930-1934)分别用不同的方法对代数体函数建立了相当于亚纯函数奈望林纳理论的基本定理,即代数体函数的第一基本定理和第二基本定理。根据第二基本定理可以得到代数体函数的亏量关系以及重值和惟一性定理等重要结果。1933年,嘉当(Cartan,H.)讨论了p(≥2)个全纯函数的线性组合a1g1(z)+a2g2(z)+…+apgp(z)的零点分布问题。特别地,当取aj=a(j=1,2,…,p=ν+1)时,则相当于考虑ν值代数体函数的值分布.因此嘉当的讨论能导出代数体函数的基本结果。
奈望林纳
芬兰数学家。1895年10月22日生于约恩苏,1980年5月28日卒于赫尔辛基。13岁时进入弦乐学校,1913年考入赫尔辛基大学学习数学,受教于林德勒夫,1917年获哲学硕士学位,1919年又取得哲学博士学位。1922年任赫尔辛基大学讲师,后任中学教师。1924年受兰道的邀请去格廷根访问,并成为兰道的助手。同年,成为芬兰科学院院士,1926年成为教授。1926年至1940年间在赫尔辛基大学任教授,1941—1945年任该校校长,之后一直在赫尔辛基大学任教,其中1959年至1962年间任国际数学联盟主席,还曾担任芬兰数学会主席。德国格廷根、匈牙利科学院院士,瑞典皇家科学院、丹麦科学院外籍院士等。
奈望林纳的兴趣十分广泛,如音乐、古典文学、数学。在数学上他是芬兰现代数学的奠基者,其主要贡献在解析函数论领域,他还是现代亚纯函数理论的创始人。1918—1919年,他开始研究亚纯函数,1921年对星形单叶函数得到了精确的系数估计,20年代发表的亚纯函数数值分布理论的基本定理,奠定了这一分支的基础。这一理论被誉为奈望林纳的值分布理论。以后他发展了这个理论,给出了第一及第二基本定理,由此推出亚纯函数值分布的一系列结果,H·外尔认为这是“本世纪为数很少的重大数学事件之一”。此外,他在超越整函数、黎曼曲面分类理论、单位圆盘上的单叶函数、开黎曼面上的阿贝尔积分等方面都有研究工作。其他成就包括创立了调和测度与相伴原理,以及哈达马三圆定理的推广、弹道的测定等。
奈望林纳一生在许多不同论题上不断地写了大量的文章与书,写有名著《解析函数论》(1936,有多种文字译本)、《皮卡-波莱尔定理与亚纯函数理论》(1929)及《单值解析函数》(1935)、《单值化》(有中译本)、《黎曼曲面》(1953)、《无坐标分析学》(1959)、《复分析综合讲义》(1966)等。他先后被海德堡等6所大学授予名誉博士称号。并获国际威赫里(Wihuri)奖(1958)和北欧的斯蒂芬斯(Henrik Steffens)奖,还曾得到芬兰的白玫瑰大十字勋章。他是芬兰雄狮勋章一级勋爵士,还获得二级自由十字勋章。

-
非线性方程组数值解法
2025-10-31 17:10:12 查看详情


 求购
求购










