- 等价无穷小

等价无穷小
数学定义
 等价无穷小(3)等价无穷小的定义:设当
等价无穷小(3)等价无穷小的定义:设当![]() 时,
时,![]() 和
和![]() 均为无穷小量。若
均为无穷小量。若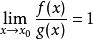 ,则称
,则称![]() 和
和![]() 是等价无穷小量,记作
是等价无穷小量,记作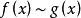
 。
。
例如:由于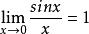 ,故有
,故有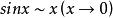 。
。
等价无穷小替换是计算未定型极限的常用方法,它可以使求极限问题化繁为简,化难为易。
求极限时,使用等价无穷小的条件[2]:
- 被代换的量,在取极限的时候极限值为0;
- 被代换的量,作为被乘或者被除的元素时可以用等价无穷小代换,但是作为加减的元素时就不可以。
替换定理
无穷小等价替换定理[3]
设函数![]() ,
,![]() ,
,![]() ,在
,在![]() 内有定义,且有
内有定义,且有
![]()
(1)若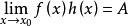 ,则
,则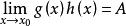 ;
;
(2)若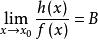 ,则
,则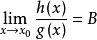 。
。
证明:
(1)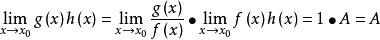 。
。
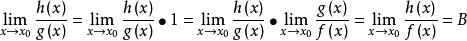 。
。
例如:利用等价无穷小量代换求极限
![]() 解:由于
解:由于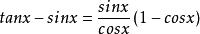 ,
,
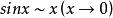 ,
,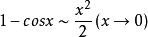 ,
,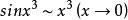 ,
,
故有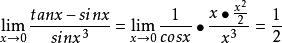 。
。
注意:等价无穷小一般只能在乘除中替换,在加减中替换有时会出错(加减时可以整体代换,不一定能随意单独代换或分别代换)[2]。如在上例中:
若因有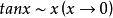 ,
,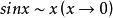 ,而推出
,而推出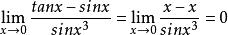 ,则得到的是错误的结果。
,则得到的是错误的结果。
注:可直接等价替换的类型
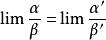
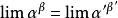
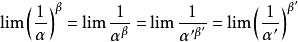
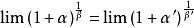
(以上几个性质可以用来化简一些未定式以方便运用洛必达法则)
需要满足一定条件才能替换的类型
若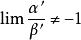 ,则
,则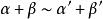
(该条性质非常重要,这是判断在加减法中能否分别等价替换的重要依据)
变上限积分函数(积分变限函数)也可以用等价无穷小进行替换。
推导公式
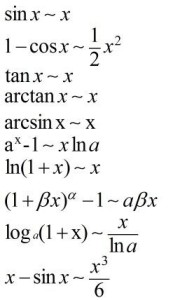 常见等价无穷小当
常见等价无穷小当![]() 时,
时,
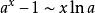
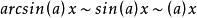
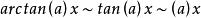
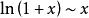
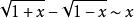
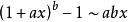
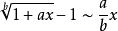
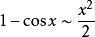
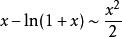
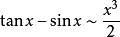
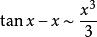
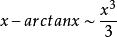
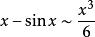
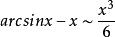
注:以上各式可通过泰勒展开式推导出来。
推导过程
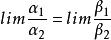 α和β都是无穷小,且
α和β都是无穷小,且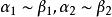 ,
,![]() 存在(或
存在(或![]() ),则有
),则有
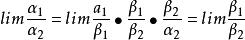 [4]
[4]
极限含义
数学分析的基础概念。它指的是变量在一定的变化过程中,从总的来说逐渐稳定的这样一种变化趋势以及所趋向的数值(极限值)。极限方法是数学分析用以研究函数的基本方法,分析的各种基本概念(连续、微分、积分和级数)都是建立在极限概念的基础之上,然后才有分析的全部理论、计算和应用.所以极限概念的精确定义是十分必要的,它是涉及分析的理论和计算是否可靠的根本问题。历史上是柯西(Cauchy,A.-L.)首先较为明确地给出了极限的一般定义。他说,“当为同一个变量所有的一系列值无限趋近于某个定值,并且最终与它的差要多小就有多小”(《分析教程》,1821),这个定值就称为这个变量的极限.其后,外尔斯特拉斯(Weierstrass,K.(T.W.))按照这个思想给出严格定量的极限定义,这就是现在数学分析中使用的ε-δ定义或ε-Ν定义等。从此,各种极限问题才有了切实可行的判别准则。在分析学的其他学科中,极限的概念也有同样的重要性,在泛函分析和点集拓扑等学科中还有一些推广。



 求购
求购






