渐开线

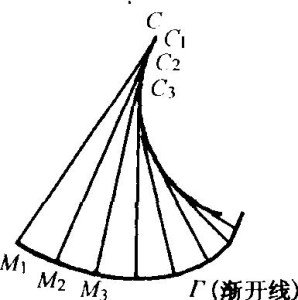图1如图1所示，与一条曲线C的所有切线相交成直角的曲线Γ，称为曲线C的渐开线；原曲线C称为(对它的任意渐开线) C1的渐屈线。同一条平面曲线(渐屈线)，有无限条渐开线。任何两条渐开线对应点的距离是常数。若曲线A是曲线B的渐开线，曲线B是曲线A的渐屈线。在曲线上只有一条渐屈线。渐开线上任一点法向压力的方向线与该点速度方向线所夹锐角称为该点的压力角。

一般的，渐开线指“圆的渐开线”。一条直线在一个圆上作无滑动的滚动时，直线上一定点运动的轨迹称为“圆的渐开线”，而称该圆为渐开线的“基圆”，直线为渐开线的“发生线”，如图2所示。即若在圆周绕有无弹性的细绳，且保持这个圆固定不动，而将细绳拉紧并逐渐展开，，让该线绕圆轴运动且始终与圆轴相切，那么线上一个定点在该平面上的轨迹就是渐开线。

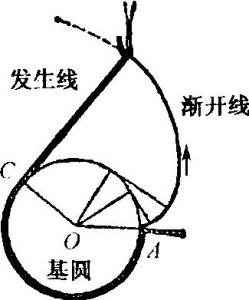图2渐开线的形状仅取决于基圆的大小，基圆越小，渐开线越弯曲；基圆越大，渐开线越平直；基圆为无穷大时，渐开线为斜直线。

机械上为了传动平稳，齿轮的齿廓线大多采用渐开线^[1]。

若基圆的半径为r，以基圆圆心为原点建立坐 标系，则可得渐开线的参数方程：

式中，为定点与圆心连线和X轴间 的夹角。

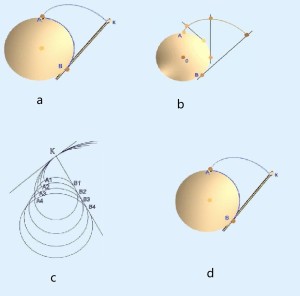图3（1）渐开线的发生线展直前后长度不变，即发生线沿基圆滚过的长度等于基圆上被滚过的弧长，如图3(a)中，弧。

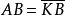（2）渐开线上任一点的法线必与基圆相切。KB为渐开线在K点的法线，发生线沿基圆作纯滚动，所以线段为渐开线上点的法线，且必与基圆相切。B是渐开线K点处的曲率中心，BK是曲率半径；A处的曲率半径为0。渐开线各点的曲率半径是变化的，K点离基圆越远，曲率半径越大，渐开线形状越平缓。如图3(b).

（3）渐开线的形状取决于基圆的大小，同一基圆上的渐开线形状完全相同。基圆越大渐开线越平直，基圆半径为无穷大时，渐开线就成为直线，即基圆半径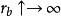，渐开线直线，如图3(c)。

（4）因渐开线是从基圆开始向外展开的，故基圆以内无渐开线；渐开线上各点压力角不相等。离基圆越远，压力角越大。如图3(d)。

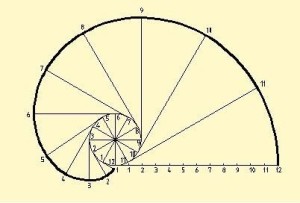图3 渐开线画法已知圆的直径D，如图4所示，画渐开线的方法为：

(1)将圆周分成若干等分(图中为12等分)，将周长πD作相同等分；

(2)过周长上各等分点作圆的切线；

(3)在第一条切线上，自切点起量取周长的一个等分（πD/12）得点1；在第二条切线上，自切点起量取周长的两个等分（2xπD/12）得点2；依此类推得点3、4、……、12；

(4)用曲线板光滑连接点1、2、3、……、12。即得圆的渐开线。