- 除以零

除以零
基本算术
基本算术中,除法指将一个集合中的物件分成若干等份。例如,个苹果平分给
人,每人可得
个苹果。同理,
个苹果只分给
人,则其可独得
个苹果。
若除以又如何?若有
颗苹果,无人来分,每“人”可得多少苹果?问题本身是无意义的,因根本无人来,论每“人”可得多少,根本多余。因此,
,在基本算术中,是无意义或未下定义的。
另种解释是将除法理解为不断的减法。例如“除以
”,换一种说法,
减去两个
,余下
,即被除数一直减去除数直至余数数值低于除数,算式为
余数
。若某数除以零,就算不断减去零,余数也不可能小于除数,使得算式与无穷拉上关系,超出基本算术的范畴。此解释也有一问题,即为无穷大乘以零仍是零。
早期尝试
婆罗摩笈多(598–668年)的著作《Brahmasphutasiddhanta》被视为最早讨论零的数学和定义涉及零的算式的文本。但当中对除以零的论述并不正确,根据婆罗摩笈多,
| “ | 一个正或负整数除以零,成为以零为分母的分数。零除以正或负整数是零或以零为分子、该正或负整数为分母的分数。零除以零是零。 | ” |
830年,摩诃吠罗在其著作《Ganita Sara Samgraha》试图纠正婆罗摩笈多的错误,但不成功:
| “ | 一数字除以零会维持不变。 | ” |
婆什迦罗第二尝试解决此问题,设,虽然此定义有一定道理,但会导致一个悖论:
的结果可以是任意一个数,那么就会得出所有的数都相同的错误结论。
 安卓手机计算器除以0显示无限大
安卓手机计算器除以0显示无限大
代数处理
| “ | 一个正或负整数除以零,成为以零为分母的分数。零除以正或负整数是零或以零为分子、该正或负整数为分母的分数。零除以零是零。 | ” |
除以零的谬误
| “ | 一数字除以零会维持不变。 | ” |
虚假的除法
若某数学系统遵从域的公理,则在该数学系统内除以零必须为没有意义。这是因为除法被定义为是乘法的逆向操作,即值是方程
中
的解(若有的话)。若设
,方程
可写成
或直接
。因此,方程
没有解(当
时),但
是任何数值也可解此方程(当
时)。在各自情况下均没有独一无二的数值,所以
未能下定义。
数学分析
在代数运算中不当使用除以零可得出无效证明:由:
得出:
除以零得出
简化,得出:
以上谬论假设,就是某数除以0是容许的并且。另一个简洁的证明
通过上面的过程,能够证明一切数字等于。但是因为不能够除以
(
),所以这个毁灭数字的过程不正常。
扩展的实数轴
在矩阵代数或线性代数中,可定义一种虚假的除法,设,当中
代表
的虚构倒数。这样,若
存在,则
。若
,则
;参见广义逆。
形式推算
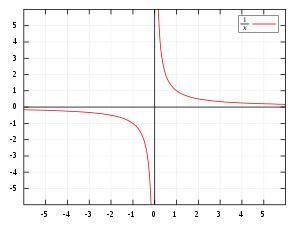 倒数函数: y = 1/x.对除了0的每一x值,y即为其倒数
倒数函数: y = 1/x.对除了0的每一x值,y即为其倒数
黎曼球
表面看来,可以藉着考虑随着趋向
的
极限而定义
。对于任何正数
,
而对于任何负数,
所以,对于正数,
可被定义为
,而对于负数
则可定义为
。不过,某数也可以由负数一方(左面)趋向零,这様,对于正数
,
定义为
,对于负数
,
定义为
。由此可得(假设实数的基本性质可应用在极限上):
最终变成 ,与在扩展的实数轴上对极限赋予的标准定义不相符。唯一的办法是用没有正负号的无限,参见下面。
另外,利用极限的比无为提供解释:
并不存在,而
若随着趋向
,
与
均趋向
,该极限可等于任何实数或无限,或者根本不存在,视乎
及
是何函数(参阅洛必达法则)。由此,
难以被定义为一极限。

-
路程除以耗油量等于什么
2025-09-21 09:28:21 查看详情


 求购
求购

