- 复形

复形
基本介绍
单纯复形(simplicial complex)亦称几何单纯复形,是单纯同调论中的一个基本概念,是用单形构造的并且按一定规则组成的图形,它是定义一类拓扑空间的工具。
下面用单形构造更复杂的图形——复形:
定义K是单形的有限集合。如果K满足
(1) 若![]() 是K的单形,则
是K的单形,则![]() 的任意面都属于K;
的任意面都属于K;
(2) K中所有有单形都规则相处(见下文“规则相处”的介绍);
那么称K为单纯复形,简称复形。K中单形维数的最大值为K的维数,记作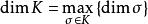 ,K的零维单形称为K的顶点[1]。
,K的零维单形称为K的顶点[1]。
单纯复形的连通性
单纯复形的连通性(connectivity of simplicial complex)是拓扑空间的连通性在复形上的推广。若复形K不是两个非空不相交的子复形的并集,则称复形K是连通的。若L是复形K的连通子复形,并且L不是任何其他连通子复形的真子复形(实际上L是K的极大的连通子复形),则称L为K的一个连通分支,复形K的连通性等价于下列各条件[2]:
1.对于复形K中任意顶点a与b,存在K的一系列顶点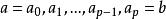 ,使得
,使得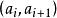 都是K的1维单形
都是K的1维单形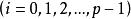 。
。
2.复形K的多面体![]() 是道路连通的。
是道路连通的。
3.复形K的多面体![]() 是连通的。
是连通的。
任意复形K都是有限个互不相交的连通分支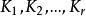 的并,因此多面体
的并,因此多面体![]() 是相同个数互不相交的连通分支
是相同个数互不相交的连通分支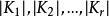 的并,若单纯复形K是
的并,若单纯复形K是![]() 个连通分支
个连通分支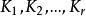 的并集,则各维同调群
的并集,则各维同调群![]() 有下列直和分解
有下列直和分解
![]() 对于零维同调群,当复形K是连通复形时,
对于零维同调群,当复形K是连通复形时,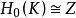 ,这里Z是整数加群。而当复形K是r个连通分支的并集时,
,这里Z是整数加群。而当复形K是r个连通分支的并集时,![]() 是r个整数加群Z的直和,即
是r个整数加群Z的直和,即
![]()
相关定义与定理
单纯形
设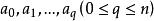 是Rn中的点,若
是Rn中的点,若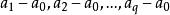 具有线性关系,则说明这一组点占有最广的位置。当
具有线性关系,则说明这一组点占有最广的位置。当![]() 时就是一个点,自然此点占有最广位置[1]。
时就是一个点,自然此点占有最广位置[1]。
单纯形
设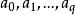 是Rn中占有最广位置的
是Rn中占有最广位置的![]() 点,而
点,而![]() ,则我们称点
,则我们称点![]() 的集合
的集合
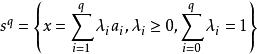 为q维单纯形,简称q维单形,
为q维单纯形,简称q维单形,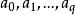 称为
称为![]() 顶点,故常将
顶点,故常将![]() 记作
记作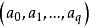 ,而系数
,而系数![]() 称为此单纯形的重心坐标。
称为此单纯形的重心坐标。
定义对于q维单形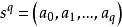 ,称
,称![]() 的(
的(![]() )个顶点中的
)个顶点中的![]() 个点
个点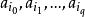 所构成的
所构成的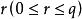 维单形
维单形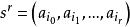 为
为![]() 的一个r维面,
的一个r维面,![]() 的0维面就是顶点,把1维面称为棱。
的0维面就是顶点,把1维面称为棱。
例1考虑3维单形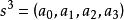 ,对于点
,对于点![]() ,就有
,就有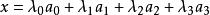 ,
,
![]()
例如,![]() 维面,
维面,![]() 为棱,
为棱,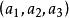 为面,
为面,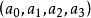 为体,如图1所示。
为体,如图1所示。
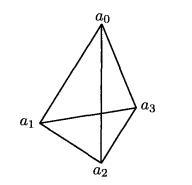 图1 3维单形(四面体)
图1 3维单形(四面体)
有向单形与无向单形
当![]() 时,
时,![]() 的
的![]() 点有
点有![]() 个排列,它们决定同一个
个排列,它们决定同一个![]() ,这样的单形
,这样的单形![]() 被称为无向单形,在
被称为无向单形,在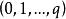 排列中,有一半是偶置换,一半是奇置换,因而这两个置换等价类构成了
排列中,有一半是偶置换,一半是奇置换,因而这两个置换等价类构成了![]() 两个定向,指定一个定向单形称为有向单形,简记“
两个定向,指定一个定向单形称为有向单形,简记“![]() ”=
”=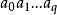 ,这里指顶点次序为
,这里指顶点次序为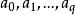 的有向单形;另一个定向单形记作“
的有向单形;另一个定向单形记作“![]() ”=
”=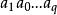 ,以单纯形作为构件,可以组成单纯复合形、多面体和链。
,以单纯形作为构件,可以组成单纯复合形、多面体和链。
单纯复合形(复形)
如果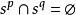 或是一个公共面,则单形
或是一个公共面,则单形![]() 和
和![]() 是规则相处的,如图2所示,否则是不规则相处的,如图3所示。
是规则相处的,如图2所示,否则是不规则相处的,如图3所示。
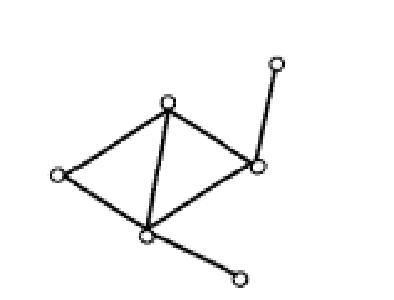 图2 规则相处
图2 规则相处
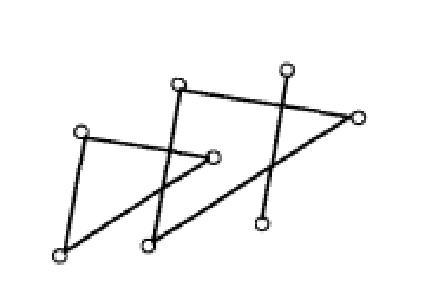 图3 不规则相处
图3 不规则相处
设W是Rn中有限个单形集合,如果W满足下列两个条件:
(1)如果![]() ,
,![]() 的任一面也属于W;
的任一面也属于W;
(2)W的任意两个单形![]() 和
和![]() 规则相处,
规则相处,
则称W为单纯复合形,简称为复形,如图4所示;否则是非复形,如图5所示[3]。
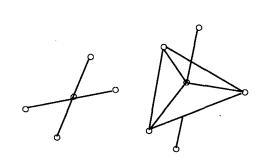 图4 复形
图4 复形
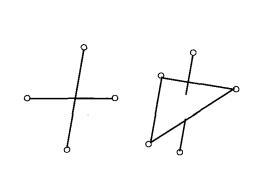 图5 非复形
图5 非复形
有向单形的基本组
设W是一个n维复形,它的全体无向单形
![]() 都己任意地规定了一个定向,这里
都己任意地规定了一个定向,这里![]() 为W中q维单形的个数,这样,得到一组有向单形
为W中q维单形的个数,这样,得到一组有向单形
![]() 上式称为W的有向单形的基本组。
上式称为W的有向单形的基本组。
链
设![]() 为n维复形W的一个基本组,对于
为n维复形W的一个基本组,对于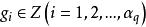 ,形式地定义
,形式地定义
![]()
![]() 称为W的一个q维链。
称为W的一个q维链。
1维链可看作是有向的折线[3]。
链边界
如果把边界算子![]() 扩展到有向单形和复形上去,则有下面的链边界。
扩展到有向单形和复形上去,则有下面的链边界。
定义对于任意q维有向单形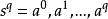 ,我们定义(
,我们定义(![]() )维链
)维链![]() :
:
![]()
![]() 称之为
称之为![]() 的边界链或简称边界。式中
的边界链或简称边界。式中![]() 表示缺
表示缺![]() 这一点,也可以把
这一点,也可以把![]() 扩展到W的q维链
扩展到W的q维链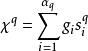 上去,定义W的任意q维链
上去,定义W的任意q维链![]() 的边界为
的边界为
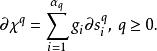 由此可见,边界算子
由此可见,边界算子![]() 建立了链群
建立了链群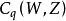 到
到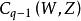 的一个同态[3]:
的一个同态[3]:
![]()



 求购
求购
