积差相关

积差相关(Pearson Product Moment Correlation Coefficient)是Pearson建立起来的、应用最广泛的相关分析技术。它以相关系数的形式较为准确地反应了两个变量之间的线性相关程度。一般来说，用积差相关计算相关系数的数据要满足以下条件：

(1)两个变量都是由测量获得的连续型数据；

(2)两个变量的总体都是呈正态分布，或接近正态分布，至少是单峰对称分布；

(3)必须是成对的数据，即两个变量应来自对同一总体或样本的测量；

(4)两个变量之间呈线性关系；

(5)大样本，n≥30^[2]。

协方差(covariance)是积差相关系数的基础。协方差表示两个随机变量在多大程度上拥有相同的方差，是两个变量的离差乘积之和除以n所得之商。其计算公式如下：

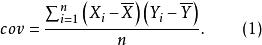
当X与Y存在严格的线性关系时，数据的协方差可能达到最大值；当X与Y之间没有关系或它们的关系不能用一条直线来描述时，协方差等于0。协方差本身没有实际的意义，将它作为一个描述性的统计量，除以两个变量的标准差，便可算得相关系数：

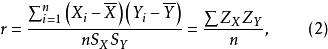其中，是变量X的标准差，是变量Y的标准差。

从公式2也可看出，其实就是两个随机变量的标准分数相乘后累加，最后再除以n。这正好说明了含义，一个较大的值说明每一个个体或者事件在两个随机变量上获得大约相等值，也就是X和Y变量在各自的分布中大致位于相同的位置。

注意点：

(1) 相关系数不是等距或等比变量，它是顺序变量。因此它只能比较大小，但不能直接做加、减、乘、除运算。比如，不能认为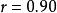的相关强度是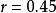的两倍，或者直接进行加减运算。

(2) 相关系数反映了变量间共变关系的密切程度，介于-1到1之间。正负号代表相关的性质，绝对值大小则反映了变量间的相关程度^[2]。

相关系数的显著性检验的目的是用样本相关系数推断总体是否相关。由于相关系数是根据样本数据计算出来的，它会受到样本波动的影响。能否根据样本相关系数来说明总体的相关系数呢?这就需要考察样本相关系数的可靠性，也就是进行显著性检验。

就Pearson相关系数来说，它符合自由度为的分布，该检验可用于小样本，也可用于大样本，检验的具体步骤如下：

第1步：提出假设：

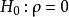即总体相关系数等于0；

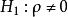即总体相关系数不等于0。

第2步：计算检验的统计量：

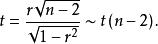
第3步：进行决策。

求出统计量的p值，如果，则拒绝，表明总体的两个变量之间存在显著的线性关系^[2]。