- 倾斜观测

倾斜观测
方法
倾斜仪观测法 常见的倾斜仪有水准管式倾斜仪、气泡式倾斜仪和电子倾斜仪等。 倾
 斜仪一般具有能连续读数、自动记录和数字传输等特点,有较高的观测精度,因而在倾斜观测中得到广泛应用。下面就气泡式倾斜仪作简单介绍。 气泡式倾斜仪由一个高灵敏度的气泡水准管e和一套精密的
测微器组成。气泡水准管固定 在架a上,可绕c转动,a下装一
弹簧片d,在底板b下为置放装置m,测微器中包括测微杆g、读数盘h和指标k。将倾斜仪安置在需要的位置上,转动读数盘,使测微杆向上(向下)移动,直至水准管气泡居中为止。此时在读数盘上读数,即可得出该处的倾斜度。 我国制造的气泡式倾斜仪灵敏度为2″,总的观测范围为1°。气泡式倾斜仪适用于观测较大的
倾斜角或量测局部地区的变形,例如:测定设备基础和平台的倾斜等。
斜仪一般具有能连续读数、自动记录和数字传输等特点,有较高的观测精度,因而在倾斜观测中得到广泛应用。下面就气泡式倾斜仪作简单介绍。 气泡式倾斜仪由一个高灵敏度的气泡水准管e和一套精密的
测微器组成。气泡水准管固定 在架a上,可绕c转动,a下装一
弹簧片d,在底板b下为置放装置m,测微器中包括测微杆g、读数盘h和指标k。将倾斜仪安置在需要的位置上,转动读数盘,使测微杆向上(向下)移动,直至水准管气泡居中为止。此时在读数盘上读数,即可得出该处的倾斜度。 我国制造的气泡式倾斜仪灵敏度为2″,总的观测范围为1°。气泡式倾斜仪适用于观测较大的
倾斜角或量测局部地区的变形,例如:测定设备基础和平台的倾斜等。
 斜仪一般具有能连续读数、自动记录和数字传输等特点,有较高的观测精度,因而在倾斜观测中得到广泛应用。下面就气泡式倾斜仪作简单介绍。 气泡式倾斜仪由一个高灵敏度的气泡水准管e和一套精密的
测微器组成。气泡水准管固定 在架a上,可绕c转动,a下装一
弹簧片d,在底板b下为置放装置m,测微器中包括测微杆g、读数盘h和指标k。将倾斜仪安置在需要的位置上,转动读数盘,使测微杆向上(向下)移动,直至水准管气泡居中为止。此时在读数盘上读数,即可得出该处的倾斜度。 我国制造的气泡式倾斜仪灵敏度为2″,总的观测范围为1°。气泡式倾斜仪适用于观测较大的
倾斜角或量测局部地区的变形,例如:测定设备基础和平台的倾斜等。
斜仪一般具有能连续读数、自动记录和数字传输等特点,有较高的观测精度,因而在倾斜观测中得到广泛应用。下面就气泡式倾斜仪作简单介绍。 气泡式倾斜仪由一个高灵敏度的气泡水准管e和一套精密的
测微器组成。气泡水准管固定 在架a上,可绕c转动,a下装一
弹簧片d,在底板b下为置放装置m,测微器中包括测微杆g、读数盘h和指标k。将倾斜仪安置在需要的位置上,转动读数盘,使测微杆向上(向下)移动,直至水准管气泡居中为止。此时在读数盘上读数,即可得出该处的倾斜度。 我国制造的气泡式倾斜仪灵敏度为2″,总的观测范围为1°。气泡式倾斜仪适用于观测较大的
倾斜角或量测局部地区的变形,例如:测定设备基础和平台的倾斜等。
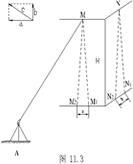
1.一般投点法 1.一般建筑物的倾斜观测 对需要进行倾斜观测的一般建筑物,要在几个侧面观测。如图11.3,在距离墙面大于墙高的地方选一点A 安置 经纬仪瞄准墙顶一点M,向下投影得一点M1,并作标志。过一段时间,再用经纬仪瞄准同一点M, 向下投影得M2点。若建筑物沿侧面方向发生倾斜,M点已移位,则M1点与M2点不重合,于是量得水平偏移量a。同时,在另一侧面也可测得偏移量b,以H代表建筑物的高度,则建筑物的倾斜度为: i=[√(a2+b2)]/H (11.1) 2.锥形建筑物的倾斜观测 当测定圆形建筑物,如烟囱、水塔等的倾斜度时,首先要求得顶部中心O′点 图11.3 v对底部中心O 点的偏心距。其做法如下。 在烟囱底部边沿平放一根标尺,在标尺的 垂直平分线方向上安置经纬仪,使经纬仪距烟 囱的距离不小于烟囱高度的1.5倍。用望远镜瞄准底部边缘两点A、A′及顶部边缘两点B、B′,并分别投点到标尺上,设读数为y1、y1′ 和y2 、y2′ ,则烟囱顶部中心O′点对底部中心O点在y 方向的偏心距: δy=(y2+y'2)/2-(y1+y'1)/2 (11.2) 同法再安置经纬仪及标尺于烟囱的另一垂直方向( 方向),测得底部边缘和顶部边缘在标尺上投点读数为x1 、x1 ′和 x2、x2′ ,则在x 方向上的偏心距为: δx=(x2+x'2)/2-(x1+x'1)/2 (11.3) 烟囱的总偏心距为 : δ=√(δ2x+δ2y)(11.4) 烟囱的倾斜方向为 : vαoo'=arctan-1(δy/δx )(11.5) 式中: α为以 轴作为标准方向线所表示的 方向角。 以上观测,要求仪器的水平轴应严格水平。因此,观测前仪器应进行检验与校正,使观测误差在允许误差范围以内,观测时应用正 倒镜观测两次取其平均值。

相关百科


 求购
求购










