内插

按特定函数的性质分，有线性内插、非线性内插等；

按引数(自变量)个数分，有单内插、双内插和三内插等。

我国古代早就发明了内插法，当时称为招差术。如公元前1世纪左右的《九章算术》中的“盈不足术”即相当于一次差内插(线性内插)；隋朝作《皇极历》的刘焯发明了二次差内插(抛物线内插)；唐朝作《太衍历》的僧一行又发明了不等间距的二次差内插法；元朝作《授时历》的郭守敬进一步发明了三次差内插法^[1]。在刘焯1000年后，郭守敬400年后，英国牛顿才提出内插法的一般公式。

内插：

假设一组已知的数据其型态为

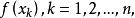
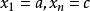
假设某些点并不属于上述的型态，但是，如果我们要估计这些点的函数值就须要做内插(interpolation)。我们可以视原数据所描述的函数复杂程度来选择不同的数值内插方法。

内插法，一般是指数学上的直线内插^[2]，利用等比关系，是用一组已知的未知函数的自变量的值和与它对应的函数值来求一种求未知函数其它值的近似计算方法，是一种未知函数，数值内插法逼近求法。天文学上和农历计算中经常用的是白塞尔内插法，可参考《中国天文年历》的附录。另外还有其他非线性内插法：如二次抛物线法和三次抛物线法。因为是用别的线代替原线，所以存在误差。可以根据计算结果比较误差值，如果误差在可以接受的范围内，才可以用相应的曲线代替。一般查表法用直线内插法计算。

数学内插法即“直线插入法”，其原理^[2]为：

若A(i1,b1),B(i2,b2)为两点，则点P（i,b)在上述两点确定的直线上；而工程上常用的为i在i1,i2之间，从而P在点A、B之间，故称“直线内插法”。

数学内插法说明点P反映的变量遵循直线AB反映的线性关系。

易得，A、B、P三点共线，则(b-b1)/(i-i1)=（b2-b1)/(i2-i1)=直线斜率，变换即得所求。

线性内插是假设在二个已知数据中的变化为线性关系，因此可由已知二点的坐标(a,b)去计算通过这二点的斜线，公式如下：

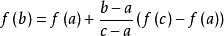
其中a<b<c在上式的b点即是代表要内插的点，f(b)则是要计算的内插函数值。

语法结构为YI=interp1(X,Y,XI),其中X,Y为已知数据，XI为要插值的数据点。如果语法结构为YI=interp1(X,Y,XI,'method'),其中method可以为linear,nearest,cubic,spline等表示线性、最近、立方、样条差值。

二维内插与一维内插的区别是二维内插数据为二维。

语法结构为interp2(X,Y,Z,XI,YI),其中X,Y,Z为已知数据,Z=Z(X,Y),而XI,YI为要插值的数据点;如果语法结构为interp2(X,Y,Z,XI,YI,'method'),其中method可以为linear,cubic表示线形或三次方插值。

它可以用interp1指定内插方式为spline来做。另一种方式也可以用spline(x,y,xi)来做，其中的x,y,xi的用法与interp1中的语法相同。事实上这二种方法采用相同的spline函数做运算，也就是当我们执行interp1(x,y,xi,'spline')时，MATLAB即呼叫spline(x,y,xi)做运算，再将计算结果传回interp1。