- 电子自旋

电子自旋
电子自旋定义
电子自旋
spin of the electron
电子的基本性质之一。电子内禀运动或电子内禀运动量子数的简称。1925年G.E.乌伦贝克和S.A.古兹密特受到泡利不相容原理的启发,分析原子光谱的一些实验结果,提出电子具有内禀运动——自旋,并且有与电子自旋相联系的自旋磁矩。由此可以解释原子光谱的精细结构及反常塞曼效应。电子的自旋角动量如图,式中电子自旋S= 1/2。1928年P.A.M.狄拉克提出电子的相对论波动方程,方程中自然地包括了电子自旋和自旋磁矩。电子自旋是量子效应,不能作经典的理解,如果把电子自旋看成绕轴的旋转,则得出与相对论矛盾的结果。
电子自旋性质
进一步研究表明,不但电子存在自旋,中子、质子、光子等所有微观粒子都存在自旋,只不过取值范围不同。自旋和静质量、电荷等物理量一样,也是描述微观粒子固有属性的物理量。在电子自旋的学习中,首先要了解电子自旋的实验依据及自旋假设,重点掌握电子自旋的描述,同时能应用电子自旋的理论解释原子光谱现象。
因为电子有1/2的自旋,所以在外加磁场下能级二分。当外加具有与此能量差相等的频率电磁波时,便会引起能级间的跃迁。此现象称为电子自旋共振。缩写为ESR。对相伴而产生的电磁波吸收称ESR吸收。产生ESR的条件为νo(MHz)=1.4·g·Ho(高斯)。式中νo为电磁波的频率,Ho为外部磁场强度,g为格朗因子、g因子(g factor)或g值。一个分子中有多数电子,一般说每二个其自旋反相,因此互相抵消,净自旋常为0。但自由基有奇数的电子,存在着不成对的电子(其无与之相消的电子自旋)。也有的分子虽然具有偶数的电子,但二个电子自旋同向,净自旋为一(例如氧分子)。原子和离子也有具有净自旋的,Cu2+、Fe3+、和Mn2+等常磁性离子即是。这些原子和分子为ESR研究的对象。由于电子自旋与原子核的自旋相互作用,ESR可具有几条线的结构,将此称为超微结构(hyperfine structure)。g因子及超微结构都有助于了解原子和分子的电子详细状态。也可鉴定自由基。另外,从ESR吸收的强度可进行自由基等的定量。因为电子自旋的缓和依赖于原子及分子的旋转运动,所以通过对ESR的线宽测定,可以了解原子及分子的动的状态。[1]
虽然原理类似于核磁共振,但由于电子质量远轻于原子核,而有强度大许多的磁矩。以氢核(质子)为例,电子磁矩强度是质子的659.59倍。因此对于电子,磁共振所在的拉莫频率通常需要透过减弱主磁场强度来使之降低。但即使如此,拉莫频率通常所在波段仍比核磁共振拉莫频率所在的射频范围还要高——微波,因而有穿透力以及对带有水分子的样品有加热可能的潜在问题,在进行人体造影时则需要改变策略。举例而言,0.3 特斯拉的主磁场下,电子共振频率发上在8.41吉赫,而对于常用的核磁共振核种——质子而言,在这样强度的磁场下,其共振频率为12.77 兆赫。
值得注意的是,电子的自旋只有一种状态,所谓的的+1/2和-1/2的自旋是自旋在z轴方向上的投影。
电子自旋应用
自旋的直接应用包括电子顺磁共振谱(EPR)、巨磁电阻硬盘磁头、自旋场效应晶体管等。[2]
以电子自旋为研究对象,法阵创新磁性材料和器件的学科分支称为自旋电子学。
EPR用在造影上,理想上是可以用在定位人体中所具有的自由基,理论上较常出现在发炎病灶;但截止至2013年仍处在开发阶段,包括信噪比等等问题待解决。
数学表示
量子力学中关于自旋的数学表示
量子力学中自旋的算符为[3]
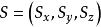 其中
其中
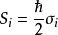 对于电子,
对于电子,![]() 是泡利矩阵:
是泡利矩阵:
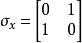
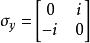
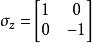
自旋算符满足

其中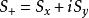 称为升算符,
称为升算符,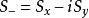 称为降算符。
称为降算符。
每个方向上电子都具有两个本征值![]() 和
和![]() ,相应的本征矢为:
,相应的本征矢为:
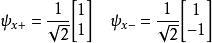
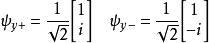
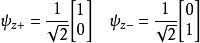
因此
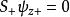
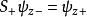
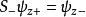
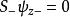 由于泡利矩阵不对易,因此各个方向测量自旋是不相容的。特别的,
由于泡利矩阵不对易,因此各个方向测量自旋是不相容的。特别的,
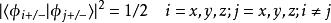 这可以用来解释在x轴方向自旋为
这可以用来解释在x轴方向自旋为![]() 的电子经过y轴方向测量时,各有
的电子经过y轴方向测量时,各有![]() 的概率测到自旋为
的概率测到自旋为![]() 和
和![]() ;之后再次在x轴轴测量,各有
;之后再次在x轴轴测量,各有![]() 的概率测到自旋为
的概率测到自旋为![]() 和
和![]() 。
。
在狄拉克方程中,自旋不再是一个好的量子数。

-
华中科技大学光学与电子信息学院
2025-09-28 16:19:08 查看详情 -
电子科技大学(沙河校区)
2025-09-28 16:19:08 查看详情 -
Jin Air Green Wings电子竞技俱乐部
2025-09-28 16:19:08 查看详情 -
杭州电子信息职业学校
2025-09-28 16:19:08 查看详情 -
云南师范大学物理与电子信息学院
2025-09-28 16:19:08 查看详情


 求购
求购









