半立方抛物线

半立方抛物线（cuspidal cubic）是一个参数式如下的平面代数曲线

其隐方程为

可以求得y得到以下的式子

此三次平面曲线在原点有一尖点。

有一种特殊的半立方抛物线，是抛物线的渐屈线，其方程式为

若将Tschirnhausen cubic catacaustic展开，可以证明也是半立方抛物线：

半立方抛物线的另一个特性是其为等时曲线，也就是说一物体在其曲线上，因重力而往下移动，在相同的时间内会移动相同的距离。因此此曲线和等时降线有关，也是物体在不同的位置因重力同时往下移动，会在相同的时间到达最下方。此曲线也和最速降线问题有关，物体沿此轨迹，会从起点以最快速度到达终点。

半立方抛物线等时曲线的特性是由雅各布·伯努利为了回答戈特弗里德·莱布尼茨在1687年提出的一个挑战，在1690年提出此曲线的特性。

在代数几何中，一条代数曲线是一维的代数簇。最典型的例子是射影平面上由一个齐次多项式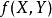定义的零点。