- 切线

切线
几何定义
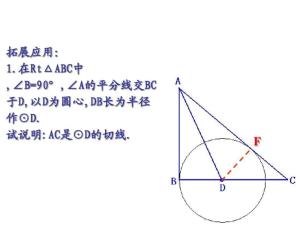 切线 P和Q是曲线C上邻近的两点,P是定点,当Q点沿着曲线C无限地接近P点时,割线PQ的 极限位置PT叫做曲线C在点P的切线,P点叫做切点;经过切点P并且垂直于切线PT的直线PN叫做曲线C在点P的法线(无限逼近的思想)
切线 P和Q是曲线C上邻近的两点,P是定点,当Q点沿着曲线C无限地接近P点时,割线PQ的 极限位置PT叫做曲线C在点P的切线,P点叫做切点;经过切点P并且垂直于切线PT的直线PN叫做曲线C在点P的法线(无限逼近的思想)
说明: 平面几何中,将和圆只有一个公共交点的直线叫做圆的切线.这种定义不适用于一般的曲线;PT是曲线C在点P的切线,但它和曲线C还有另外一个交点;相反,直线l尽管和曲线C只有一个交点,但它却不是曲线C的切线。
代数定义
 切线(3)在 高等数学中,对于一个函数,如果函数某处有 导数,那么此处的导数就是过此处的切线的斜率,该点和斜率所构成的直线就为该函数的一个切线。
切线(3)在 高等数学中,对于一个函数,如果函数某处有 导数,那么此处的导数就是过此处的切线的斜率,该点和斜率所构成的直线就为该函数的一个切线。
代数几何定义
设V为由根理想
的生成元F1,...,Fr定义的仿射簇,
为过原点与(a1,...,an)的直线,则
∩V在原点的重数为所有多项式fi(t)=Fi(ta1,...,tan)中t的最低次幂的指数。
若
∩V在p点的重数大于1,则称
为V上p点的切线。
性质和定理
切线的性质定理
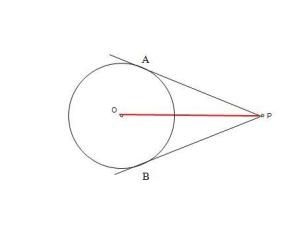 切线 圆的切线垂直于过其 切点的半径;经过半径的非圆心一端,并且垂直于这条半径的直线,就是这个圆的一条切线。
切线 圆的切线垂直于过其 切点的半径;经过半径的非圆心一端,并且垂直于这条半径的直线,就是这个圆的一条切线。
切线判定定理
一直线若与一圆有交点,且连接交点与圆心的直线与该直线垂直,那么这条直线就是圆的切线。
一般可用:
1、作垂直证半径
2、作半径证垂直
圆的切线
圆的切线的性质定理
圆的切线垂直于经过切点的半径.
推论 1:经过圆心且垂直于切线的直线必经过切点.
推论 2:经过切点且垂直于切线的直线必经过圆心.
切线的主要性质
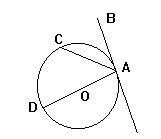 切线(1)切线和圆只有一个公共点;
切线(1)切线和圆只有一个公共点;
(2)切线和圆心的距离等于圆的半径;
(3)切线垂直于经过切点的半径;
(4)经过圆心垂直于切线的直线必过切点;
(5)经过切点垂直于切线的直线必过圆心;
(6)从圆外一点引圆的切线和 割线,切线长是这点到割线与圆交点的两条线段长的 比例中项
其中(1)是由切线的定义得到的,(2)是由直线和圆的位置关系定理得到的,(6)是由 相似三角形推得的,也就是 切割线定理。
切线的判定和性质
切线的判定定理 经过半径的外端并且垂直于这条半径的直线是圆的切线 。圆的切线垂直于这个圆过切点的半径。
几何语言:∵l ⊥OA,点A在 ⊙O上
∴直线l是⊙O的切线( 切线判定定理)
切线的性质定理 圆的切线垂直于经过切点半径
几何语言:∵OA是⊙O的半径,直线l切⊙O于点A
∴l ⊥OA(切线性质定理)
推论1 经过圆心且垂直于切线的直径必经过切点
推论2 经过切点且垂直于切线的直线必经过圆心
切线长定理
定理 从圆外一点可引出圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角
几何语言:∵弦PB、PD切⊙O于A、C两点
∴PA=PC,∠APO=∠CPO( 切线长定理)
弦切角
弦切角定理 弦切角等于它所夹的弧对的 圆周角
几何语言:∵∠BCN所夹的是 ,∠A所对的是
∴∠BCN=∠A
推论 如果两个弦切角所夹的弧相等,那么这两个弦切角也相等
几何语言:∵∠BCN所夹的是 ,∠ACM所对的是 , =
∴∠BCN=∠ACM
弦切角概念:顶点在 圆上,一边和圆相交、另一边和圆相切的角叫做弦切角.它是继 圆心角、圆周角之后第三种与圆有关的角.这种角必须满足三个条件:
(1)顶点在圆上,即角的顶点是圆的一条切线的切点;
(2)角的一边和圆相交,即角的一边是过切点的一条弦所在的射线;
(3)角的另一边和圆相切,即角的另一边是切线上以切点为 端点的一条射线.
它们是判断一个角是否为弦切角的标准,三者缺一不可,比如下图中,均不是弦切角.
(4)弦切角可以认为是 圆周角的一个特例,即圆周角的一边绕顶点旋转到与圆相切时所成的角.正因为如此,弦切角具有与圆周角类似的性质.
弦切角定理:弦切角等于它所夹的弧对的圆周角.它是圆中证明角相等的重要定理之一.
切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。
推论:从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等。

-
Chamberlain线
2025-10-31 12:04:26 查看详情 -
关于奥迪PA生产线是什么意思介绍(奥迪PA生产线是什么意思)
2025-10-31 12:04:26 查看详情


 求购
求购








