- 数量级

数量级
定义
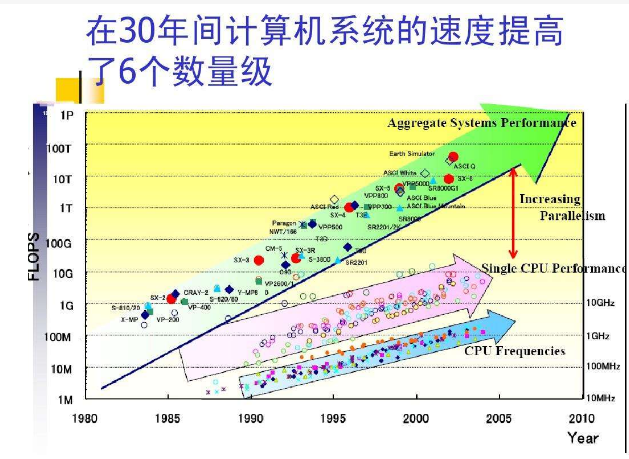 数量级(3)通常情况下,数量级指一系列 10 的幂,即相邻两个数量级之间的比为 10。例如说两数相差三个数量级,其实就是说一个数比另一个大 1000 倍。
数量级(3)通常情况下,数量级指一系列 10 的幂,即相邻两个数量级之间的比为 10。例如说两数相差三个数量级,其实就是说一个数比另一个大 1000 倍。
下面表格描述十进制下的数量级。
| 数字 | 科学记数法 | 数量级 |
|---|---|---|
| 0.001 | 10^-3 | −3 |
| 0.01 | 10^-2 | −2 |
| 0.1 | 10^-1 | −1 |
| 1 | 10^0 | 0 |
| 10 | 10^1 | 1 |
| 100 | 10^2 | 2 |
| 1000 | 10^3 | 3 |
| 10000 | 10^4 | 4 |
计算
| 数字 | 科学记数法 | 数量级 |
|---|---|---|
| 0.001 | 10^-3 | −3 |
| 0.01 | 10^-2 | −2 |
| 0.1 | 10^-1 | −1 |
| 1 | 10^0 | 0 |
| 10 | 10^1 | 1 |
| 100 | 10^2 | 2 |
| 1000 | 10^3 | 3 |
| 10000 | 10^4 | 4 |
常用
 数量级(3)一个数的数量级即它含有的 10 的幂,准确的定义为,它的常用对数的整数部分。例如,4,000,000 的对数为 6.602,它的数量级即为 6。可以这样认为,一个数的数量级就是它在对数尺度上的大致位置。
数量级(3)一个数的数量级即它含有的 10 的幂,准确的定义为,它的常用对数的整数部分。例如,4,000,000 的对数为 6.602,它的数量级即为 6。可以这样认为,一个数的数量级就是它在对数尺度上的大致位置。
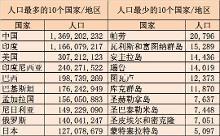
一个未知量的数量级估计即估计离它最近的 10 的幂。例如,一个在 30 亿到 300 亿之间的一个未知量(比如地球上的人口数),它的数量级可以估计为 10 。
两个量之间的数量级的差即它们相差的 10 的倍数。例如,土星的质量是地球质量的 95 倍,即土星质量比地球质量大两个数量级。
词头
常用数量级
 数量级(4)要在物理世界中把事物分类可以有很多不同的做法,其中一个方法就是比较它们的大小。本文以下的部份包括了同一数量级的事物(时间、长度、面积、体积、质量和能量)的列表,这对于了解事物的相对大小及宇宙大概的规模是很有帮助的。我们将会用到国际单位及其前缀:这些单位都包含了数量级的概念。
数量级(4)要在物理世界中把事物分类可以有很多不同的做法,其中一个方法就是比较它们的大小。本文以下的部份包括了同一数量级的事物(时间、长度、面积、体积、质量和能量)的列表,这对于了解事物的相对大小及宇宙大概的规模是很有帮助的。我们将会用到国际单位及其前缀:这些单位都包含了数量级的概念。
词条图册
国际单位制(SI)词头表示单位的倍数和分数。大多数是千的倍数或分数。
根据《中华人民共和国法定计量单位》规定,我国使用的词头如下表。括号内的字可在不致混淆的情况下省略。(10^24表示10的24次方)
| 倍数和分数 | 词头 | 符号 | 英文 |
| 10^24 | 尧(它) | Y | Yotta |
| 10^21 | 泽(它) | Z | Zetta |
| 10^18 | 艾(可萨) | E | Exa |
| 10^15 | 拍(它) | P | Peta |
| 10^12 | 太(拉) | T | Tera |
| 10^9 | 吉(咖) | G | Giga |
| 10^6 | 兆 | M | Mega |
| 10^3 | 千 | k | kilo |
| 10^2 | 百 | h | hecta |
| 10^1 | 十 | da | deca |
| 10^-1 | 分 | d | deci |
| 10^-2 | 厘 | c | centi |
| 10^-3 | 毫 | m | milli |
| 10^-6 | 微 | μ | micro |
| 10^-9 | 纳(诺) | n | nano |
| 10^-12 | 皮(可) | p | pico |
| 10^-15 | 飞(母托) | f | femto |
| 10^-18 | 阿(托) | a | atto |
| 10^-21 | 仄(普托) | z | zepto |
| 10^-24 | 幺(科托) | y | yocto |

相关百科
-
梅赛德斯 重量级缠斗
2025-10-03 20:39:30 查看详情 -
实拍全新梅赛德斯奔驰 重量级缠斗
2025-10-03 20:39:30 查看详情 -
北京市小客车数量调控暂行规定
2025-10-03 20:39:30 查看详情 -
东北财经大学数学与数量经济学院
2025-10-03 20:39:30 查看详情 -
数量经济技术经济研究
2025-10-03 20:39:30 查看详情


 求购
求购







