- 丢番图逼近

丢番图逼近
理论介绍
所谓丢番图逼近即研究种种有理逼近的一个数论分支,因为它与丢番图方程的研究密切相关,所以人们称之为丢番图逼近,或将这类问题称为丢番图分析。它还与几何学有密切关系,为此,将设置数的几何条目。中国古代对丢番图逼近上很有贡献的,例如,何承天与祖冲之就曾分别建议用22/7(约率)与355/113(密率)来近似计算圆周率π。这两个数都是π都所谓渐近分数(见连分数)。355/113的下一个渐近分数为52163/16604,再下一个为103993/33102,太复杂了。因此,密率数是π极好的有理逼近。[1]
说明
数论的一个分支,以研究数的有理逼近问题为主。这里所谓的数是指实数、复数、代数数或超越数。数的有理逼近问题,可表为求某种不等式的整数解问题。由于在整数范围求解的方程称为不定方程或丢番图方程,因而把求不等式的整数解问题称之为丢番图逼近。
1842年,P.G.L.狄利克雷首先证明了实数有理逼近的一个结果:如果α是任意实数,Q是大于1的实数,那么存在整数对p、q,满足两个不等式: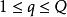 和
和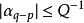 。由此可得,如果α是任意无理数,那么存在无穷多对互素的整数对p、q,满足不等式
。由此可得,如果α是任意无理数,那么存在无穷多对互素的整数对p、q,满足不等式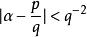 。当α是有理数时,上式不成立。
。当α是有理数时,上式不成立。
1891年,A.胡尔维茨将上式改进为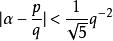 ,并指出,对于某些无理数,常数
,并指出,对于某些无理数,常数![]() 是最佳值,不可再减小。但是对于很多无理数,常数
是最佳值,不可再减小。但是对于很多无理数,常数![]() 不是最佳值,还可再减小。
不是最佳值,还可再减小。
1926年,A.Я.辛钦证明了:在勒贝格测度意义下对几乎所有的实数α,不等式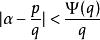 的整数解p、q有无穷多对还是只有有穷多对,由级数
的整数解p、q有无穷多对还是只有有穷多对,由级数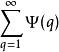 是发散的还是收敛的而定,这里ψ(q)(q>0)是正的非增函数。此即所谓丢番图逼近测度定理。例如,对几乎所有的实数α和任意的δ>0,不等式
是发散的还是收敛的而定,这里ψ(q)(q>0)是正的非增函数。此即所谓丢番图逼近测度定理。例如,对几乎所有的实数α和任意的δ>0,不等式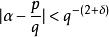 只有有穷多对整数解,而不等式
只有有穷多对整数解,而不等式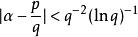 有无穷多对整数解。
有无穷多对整数解。
丢番图逼近与连分数有密切联系。一个数的连分数展开,往往就是具体构造有理逼近解的过程。例如,对于任意无理数α,有无穷多个渐近分数![]() ,满足不等式
,满足不等式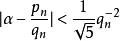 。
。
1844年,J.刘维尔开创了实代数数的有理逼近的研究,他证明了:如果α是次数为d的实代数数,那么存在一个常数C(α)>0,对于每个不等于α的有理数p/q,有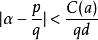 。亦即如果μ>d,那么不等式
。亦即如果μ>d,那么不等式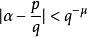 只有有穷多个解
只有有穷多个解![]() 。根据这一结果,刘维尔构造出了历史上的第一个超越数
。根据这一结果,刘维尔构造出了历史上的第一个超越数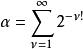 。以后一些数学家不断改进指数μ的值,直到得出μ与d无关的结果。
。以后一些数学家不断改进指数μ的值,直到得出μ与d无关的结果。
1909年,A.图埃得到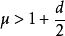 。
。
1921年,C.L.西格尔得到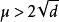 。
。
1947年至1948年间,F.戴森和A.O.盖尔丰德各自独立证明了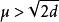 。
。
1955年,K.F.罗特得到了μ与d无关的一个结论:如果α是实代数数,其次数d≥2,那么对于任意的δ>0,不等式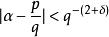 只有有穷多个解。这一结论又称为图埃-西格尔-罗特定理。
只有有穷多个解。这一结论又称为图埃-西格尔-罗特定理。
用代数数逼近代数数,也是丢番图逼近的一类重要内容。W.M.施密特所著《丢番图逼近》(1980)一书中,有详细的论述。
自20世纪以来,丢番图逼近除自身的发展外,在超越数论、丢番图方程等方面都有重要的应用。
相关介绍
刘维尔定理与 Roth 定理
刘维尔定理可用以直接构造超越数。在这之前,数学家们已藉连分数导出关于平方根与其它二次无理数的许多逼近性质。这个结果后来由 Axel Thue 等人改进,并导致 Roth 定理:将刘维尔定理中的指数 n 由代数数的次数缩减到任意的 2+ε(其中 ε>0);之后 Schmidt 将此推广到同步逼近。这些证明颇困难,而且不能得到明确的上界,这在应用上是一大缺憾。
均匀分布
取一实数序列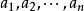 并考虑其真分数部份;或者抽象地说是考虑 R/Z,这在拓扑学上是个一维圆环 S1。对圆环上的任一段区间,我们研究有限集 {an:N<-N} 中有多大比例落在该区间,并考虑此比例与区间长度之关系。“均匀分布”意味着当 N→∞,此比例将趋近我们“期望”的值。Hermann Weyl 证明了这等价于该序列元素的指数和之上界,这表明了丢番图逼近与指数和相消的一般问题密切相关,后者在解析数论的误差项估计中无所不在。
并考虑其真分数部份;或者抽象地说是考虑 R/Z,这在拓扑学上是个一维圆环 S1。对圆环上的任一段区间,我们研究有限集 {an:N<-N} 中有多大比例落在该区间,并考虑此比例与区间长度之关系。“均匀分布”意味着当 N→∞,此比例将趋近我们“期望”的值。Hermann Weyl 证明了这等价于该序列元素的指数和之上界,这表明了丢番图逼近与指数和相消的一般问题密切相关,后者在解析数论的误差项估计中无所不在。
其它面向
在 Roth 定理以后,丢番图逼近的主要进展与超越理论相关。均匀分布关乎分布的不规则性,因而带有组合学的本性。丢番图逼近中仍有陈述简单却悬而未解的问题,例如勒特伍德猜想。



 求购
求购



