三角函数诱导公式

设α为任意角，终边相同的角的同一三角函数的值相等：

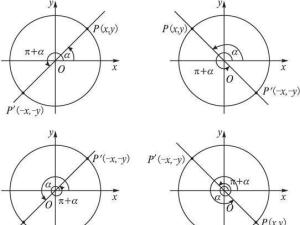三角函数诱导公式

sin（2kπ+α）=sinα （k∈Z）

cos（2kπ+α）=cosα （k∈Z）

tan（2kπ+α）=tanα （k∈Z）

cot（2kπ+α）=cotα（k∈Z）

设α为任意角，π+α的三角函数值与α的三角函数值之间的关系：

sin（π+α）=－sinα

cos（π+α）=－cosα

tan（π+α）= tanα

cot（π+α）=cotα

任意角α与-α的三角函数值之间的关系（利用 原函数 奇偶性）：

sin（－α）=－sinα

cos（－α）= cosα

tan（－α）=－tanα

cot (—α) =—cotα

利用公式二和公式三可以得到π-α与α的三角函数值之间的关系：

sin（π－α）= sinα

cos（π－α）=－cosα

tan（π－α）=－tanα

cot（π－α）=－cotα

利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系：

sin（2π-α）=－sinα

cos（2π-α）= cosα

tan（2π-α）=－tanα

cot（2π-α）=－cotα

π/2±α 及3π/2±α与α的三角函数值之间的关系：（⒈～⒋）

⒈π/2+α与α的三角函数值之间的关系

弧度制下的角的表示：

sin（π/2+α）=cosα.

cos（π/2+α）=—sinα.

tan（π/2+α）=－cotα.

cot（π/2+α）=－tanα.

sec（π/2+α）=－cscα.

csc（π/2+α）=secα. 

角度制下的角的表示：

sin（90°+α）=cosα.

cos（90°+α）=－sinα.

tan（90°+α）=－cotα.

cot（90°+α）=－tanα.

sec（90°+α）=－cscα.

csc（90°+α）=secα. 

⒉ π/2－α与α的三角函数值之间的关系

弧度制下的角的表示：

sin（π/2－α）=cosα.

cos（π/2－α）=sinα.

tan（π/2－α）=cotα.

cot（π/2－α）=tanα.

sec（π/2－α）=cscα.

csc（π/2－α）=secα.

角度制下的角的表示：

sin (90°－α)=cosα.

cos (90°－α)=sinα.

tan (90°－α)=cotα.

cot (90°－α)=tanα.

sec (90°－α)=cscα.

csc (90°－α)=secα.

⒊ 3π/2+α与α的三角函数值之间的关系

弧度制下的角的表示：

sin（3π/2+α）=－cosα.

cos（3π/2+α）=sinα.

tan（3π/2+α）=－cotα.

cot（3π/2+α）=－tanα.

sec（3π/2+α）=cscα.

csc（3π/2+α）=－secα. 

角度制下的角的表示：

sin（270°+α）=－cosα.

cos（270°+α）=sinα.

tan（270°+α）=－cotα.

cot（270°+α）=－tanα.

sec（270°+α）=cscα.

csc（270°+α）=－secα. 

⒋ 3π/2－α与α的三角函数值之间的关系

弧度制下的角的表示：

sin（3π/2－α）=－cosα.

cos（3π/2－α）=－sinα.

tan（3π/2－α）=cotα.

cot（3π/2－α）=tanα.

sec（3π/2－α）=－cscα.

csc（3π/2－α）=－secα.

角度制下的角的表示：

sin（270°－α）=－cosα.

cos（270°－α）=－sinα.

tan（270°－α）=cotα.

cot（270°－α）=tanα.

sec（270°－α）=－cscα.

csc（270°－α）=－secα. 

3π/2 ± α与α的三角函数值之间的关系：

sin（3π/2+α）=－cosα

sin（3π/2－α）=－cosα

cos（3π/2+α）=sinα

cos（3π/2－α）=－sinα

tan（3π/2+α）=－cotα

tan（3π/2－α）=cotα

cot（3π/2+α）=－tanα

cot（3π/2－α）=tanα

诱导公式记忆口诀：“奇变偶不变，符号看象限”。

“奇、偶”指的是π/2的倍数的奇偶，“变与不变”指的是三角函数的名称的变化：“变”是指正弦变余弦，正切变余切。（反之亦然成立）“符号看象限”的含义是：把角α看做锐角，不考虑α角所在象限，看n·(π/2)±α是第几象限角，从而得到等式右边是正号还是负号。以cos（π/2+α）=－sinα为例，等式左边cos（π/2+α）中n=1，所以右边符号为sinα，把α看成锐角，所以π/2<（π/2+α）<π，y=cosx在区间上小于零，所以右边符号为负，所以右边为－sinα。

符号判断口诀：

全,S,T,C,正。这五个字口诀的意思就是说：第一象限内任何一个角的四种三角函数值都是“+”；第二象限内只有正弦是“+”，其余全部是“-”；第三象限内只有正切是“+”，其余全部是“-”；第四象限内只有余弦是“+”，其余全部是“-”。

也可以这样理解：一、二、三、四指的角所在象限。全正、正弦、正切、余弦指的是对应象限三角函数为正值的名称。口诀中未提及的都是负值。

“ASTC”反Z。意即为“all(全部)”、“sin”、“tan”、“cos”按照将字母Z反过来写所占的象限对应的三角函数为正值。

另一种口诀：正弦一二切一三，余弦一四紧相连，言之为正。

万能公式推导

，

（因为）

再把分式上下同除，可得

然后用代替即可。

同理可推导余弦的万能公式。正切的万能公式可通过正弦比余弦得到。

三倍角公式推导

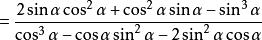
上下同除以，得：

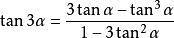
另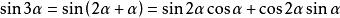

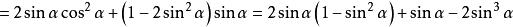
即

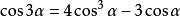
和差化积公式推导

首先，我们知道sin(a+b)=sinacosb+cosasinb，sin(a-b)=sinacosb-cosasinb，

我们把两式相加就得到sin(a+b)+sin(a-b)=2sinacosb，

同理，若把两式相减，就得到cosasinb=[sin(a+b)-sin(a-b)]/2，

同样地，我们还知道cos(a+b)=cosacosb-sinasinb，cos(a-b)=cosacosb+sinasinb，

所以，把两式相加，我们就可以得到cos(a+b)+cos(a-b)=2cosacosb，

同理，两式相减我们就得到sinasinb=-[cos(a+b)-cos(a-b)]/2，

这样，我们就得到了积化和差的公式：

cosasinb=[sin(a+b)-sin(a-b)]/2，

sinasinb=-[cos(a+b)-cos(a-b)]/2。

好，有了积化和差的四个公式以后，我们只需一个变形，就可以得到和差化积的四个公式

我们把上述四个公式中的a+b设为x，a-b设为y，那么a=(x+y)/2，b=(x-y)/2

把a,b分别用x,y表示就可以得到和差化积的四个公式:

sinx+siny=2sin[(x+y)/2]cos[(x-y)/2]

sinx-siny=2cos[(x+y)/2]sin[(x-y)/2]

cosx+cosy=2cos[(x+y)/2]cos[(x-y)/2]

cosx-cosy=-2sin[(x+y)/2]sin[(x-y)/2

同角三角函数的基本关系式

倒数关系

tanα ·cotα=1

sinα ·cscα=1

cosα ·secα=1

商的关系

sinα/cosα=tanα=secα/cscα

cosα/sinα=cotα=cscα/secα

平方关系

sin2(α)+cos2(α)=1

1+tan2(α)=sec2(α)

1+cot2(α)=csc2(α)

同角三角函数关系六角形记忆法

构造以“上弦、中切、下割；左正、右余、中间1”的正六边形为模型。

倒数关系

对角线上两个函数互为倒数；

商数关系

六边形任意一顶点上的函数值等于与它相邻的两个顶点上函数值的乘积。（主要是两条虚线两端的三角函数值的乘积，下面4个也存在这种关系。）由此，可得商数关系式。

平方关系

在带有阴影线的三角形中，上面两个顶点上的三角函数值的平方和等于下面顶点上的三角函数值的平方。

两角和差公式

sin（α + β）=sinαcosβ + cosαsinβ

sin（α - β）=sinαcosβ - cosαsinβ

cos（α + β）=cosαcosβ - sinαsinβ

cos（α - β）=cosαcosβ + sinαsinβ

tan（α + β）=(tanα + tanβ )/(1 - tanαtanβ)

tan（α - β）=(tanα - tanβ)/(1 + tanαtanβ)

二倍角的正弦余弦和正切公式

sin2α=2sinαcosα

cos2α=cos2(α) - sin2(α)=2cos2(α) - 1=1 - 2sin2(α)

tan2α=2tanα/[1 - tan2(α)]

tan[(1/2)α]=(sin α)/(1 + cos α)=(1 - cos α)/sin α

半角的正弦余弦和正切公式

sin2(α/2)=(1 - cosα)/2

cos2(α/2)=(1 + cosα)/2

tan2(α/2)=(1 - cosα)/(1 + cosα)

tan(α/2)=(1 - cosα)/sinα=sinα/1 + cosα

万能公式

sinα=2tan(α/2)/[1 + tan2(α/2)]

cosα=[1 - tan2(α/2)]/[1+tan2(α/2)]

tanα=[2tan(α/2)]/[1 - tan2(α/2)]

三倍角的正弦余弦和正切公式

sin3α=3sinα - 4sin3(α)

cos3α=4cos3(α) - 3cosα

tan3α=[3tanα - tan3(α)]/[1 - 3tan2(α)]

三角函数的和差化积公式

sinα + sinβ=2sin[(α + β)/2]cos[(α - β)/2]

sinα - sinβ=2cos[(α + β)/2]sin[(α - β)/2]

cosα + cosβ=2cos[(α + β)/2]cos[(α - β)/2]

cosα - cosβ=－2sin[(α + β)/2]sin[(α - β)/2]

三角函数的积化和差公式

sinα · cosβ=[sin(α + β) + sin(α - β)]/2

cosα · sinβ=[sin(α + β) - sin(α - β)]/2

cosα · cosβ=[cos(α + β) + cos(α - β)]/2

sinα · sinβ= - [cos(α + β) - cos(α - β)]/2

公式一到公式五函数名未改变， 公式六函数名发生改变。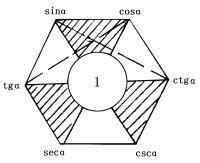三角公式的记忆图

公式一到公式五可简记为：函数名不变，符号看象限。即α+k·360°（k∈Z），﹣α，180°±α，360°-α的三角函数值，等于α的同名三角函数值，前面加上一个把α看成锐角时原函数值的符号。

三角公式的记忆图

上面这些诱导公式可以概括为：对于kπ/2±α(k∈Z)的三角函数值，

①当k是偶数时，得到α的同名函数值，即函数名不改变；

②当k是奇数时，得到α相应的余函数值，即sin→cos;cos→sin;tan→cot,cot→tan。（奇变偶不变）然后在前面加上把α看成锐角时原函数值的符号。（符号看象限）

例如：

sin(2π-α)=sin(4·π/2-α)，k=4为偶数，所以取sinα。

当α是锐角时，2π-α∈(270°，360°)，sin(2π-α)<0，符号为“-”。

所以sin(2π-α)=-sinα

奇变偶不变，符号看象限。

注：奇变偶不变（对k而言，指k取奇数或偶数），符号看象限（看原函数，同时可把α看成是锐角）。

公式右边的符号为把α视为锐角时，角k·360°+α（k∈Z），-α、180°±α，360°-α所在象限的原三角函数值的符号可记忆：水平诱导名不变；符号看象限。

各种三角函数在四个象限的符号如何判断，也可以记住口诀“一全正；二正弦(余割)；三两切；四余弦(正割)”．

这十二字口诀的意思就是说：

第一象限内任何一个角的三角函数值都是“+”；

第二象限内只有正弦和余割是“+”，其余全部是“-”；

第三象限内只有正切和余切是“+”，其余函数是“-”；

第四象限内只有正割和余弦是“+”，其余全部是“-”。

一全正，二正弦，三双切，四余弦