立方根

如果一个数的立方等于a，那么这个数叫a的立方根，也称为三次方根。也就是说，如果，那么x叫做a的立方根。^[2]

()，读作“三次根号a”，其中，a叫做被开方数，3叫做根指数。

开立方：求一个数a的立方根的运算叫做开立方。

（1）在实数范围内，任何实数的立方根只有一个

（2）在实数范围内，负数不能开平方，但可以开立方。

（3）0的立方根是0

（4）立方和开立方运算，互为逆运算。

（5）在复数范围内，任何非0的数都有且仅有3个立方根（一实根，二共轭虚根），它们均匀分布在以原点为圆心，算术根为半径的圆周上，三个立方根对应的点构成正三角形。

（2）在复数范围内，负数既可以开平方，又可以开立方。

具有大小意义的数字大小比较中：

（1）做这两个数的立方，立方数大者大

（2）作差，两数相减，若差大于0，则被减数大；若差小于0，则减数大；若差等于0，则一样大；

（3）比较被开方数，立方根大者大

立方根(3)平方根与立方根的联系与区别如下。^[2]

（1）定义不同

平方根：如果一个数的平方等于 a，那么这个数就叫 a 的平方根或二次方根．即如果，那么 x 就叫 a 的平方根；立方根：如果一个数的立方等于 a，那么这个数叫做 a 的立方根或三次方根．即如果，那么 x 叫做 a 的立方根。

（2）表示方法不同

平方根用“”表示，根指数 2 可以省略；算术平方根用“”表示，根指数 2 可以省略；立方根用“”表示，根指数 3 不能略去，更不能写成“”

（3）存在的条件不同

a 有平方根的条件：，因为正数、零、负数的平方都不是负数，故负数没有平方根和算术平方根；a 有立方根的条件：a 为全体实数，即正数、负数、零均可。

（4）结果不同

平方根的结果除0之外，有两个互为相反的结果；立方根的结果有3个（除0以外，且在复数范围内），3个立方根均匀分布在以原点为圆心，算术根为半径的圆周上，三个立方根对应的点构成正三角形。

二者都是与乘方运算互为逆运算

以下数值均取6位有效数字，正被开方数取正值，负被开方数取负值

±1：±1.00000

±2：±1.25992

±3：±1.44225

±4：±1.58740

±5：±1.70998

±6：±1.81712

±7：±1.91293

±8：±2.00000

±9：±2.08008

±10：±2.15443

±11：±2.22398

±12：±2.28943

±13：±2.35133

±14：±2.41014

±15：±2.46621

±16：±2.51984

±17：±2.57128

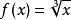的函数图像

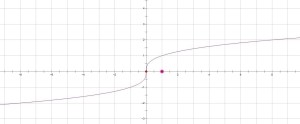函数图像

求立方根的牛顿法基于如下事实，如果y是x的立方根的一个近似值，那么下式将给出一个更好的近似值：

请利用这一公式实现一个类似平方根过程的求立方根的过程。