- 超立方体

超立方体
简介
在几何学中,超立方体是立方体的四维类比,有8个立方体胞。四维超正方体之于立方体,就如立方体之于正方形。它是四维欧式空间中6个四维凸正多胞体之一。
超正方体是一个有无穷多个成员的凸正多胞形家族的四维成员,这个家族被称为“超方形”(或称立方形、正测形),这个家族的成员与施莱夫利符号{4,3,3,……,3,3},它们都具有类似正方形和立方体的性质,如二胞角都为90°等。
超立方体这个名称在一般的场合中特指四维的这个超正方体,不过在数学上,“超立方体”这个词可以指n维(n>3)的任意一个超方形,因此把它和n维的其他超方形放在一起讨论时,要加“四维”以示区别。
几何性质
在四维欧几里得空间的标准四维方体是点(±1, ±1, ±1, ±1)的凸包。它包含了点:
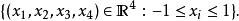
四维超立方体由八个超平面(![]() )包围。两两非平行超平面相交,共形成四维方体的24个正方形面。每条棱有3个立方体和3个正方形相交。在每一顶点有4个立方体、6个正方形和4条棱相交。四维方体共有8个立方体、24个正方形、32条棱和16个顶点。边长为a的四维超正方体超体积是
)包围。两两非平行超平面相交,共形成四维方体的24个正方形面。每条棱有3个立方体和3个正方形相交。在每一顶点有4个立方体、6个正方形和4条棱相交。四维方体共有8个立方体、24个正方形、32条棱和16个顶点。边长为a的四维超正方体超体积是![]() ,表体积是
,表体积是![]() 。
。
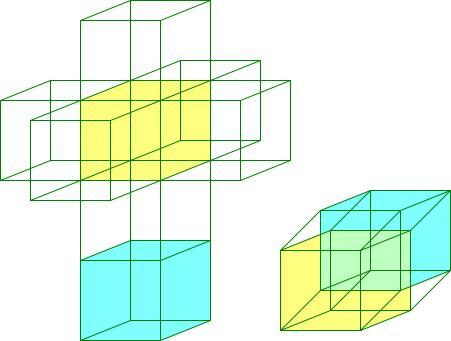 图1.四维超立方体的展开图
图1.四维超立方体的展开图
若一个四维超立方体的棱长为1,则其外接超球半径为1,外中交超球(经过超立方体各棱中点的三维超球)半径为![]() ,内中交超球(经过超立方体各面中心的三维超球)半径为
,内中交超球(经过超立方体各面中心的三维超球)半径为![]() ,内切超球半径为
,内切超球半径为![]() 。事实上,对于任意一个棱长为a的n维超方形,其自身中心到任意一个k维元素的中心的距离为
。事实上,对于任意一个棱长为a的n维超方形,其自身中心到任意一个k维元素的中心的距离为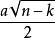 。
。
四维方体的每一顶点与4条棱相邻,所以四维方体的顶点形是正四面体。所以四维方体的施莱夫利符号是{4,3,3}。其对偶多胞体是正十六胞体,施莱夫利符号是{3,3,4}。
投影
1.二维投影
超;立方体的构造方法可以通过以下方式来想象:
- 从零维到一维:两个点A和B可以被连接起来,我们就得到一个新的线段AB。
- 从一维到二维:两个平行的线段AB和CD可以被连接起来,我们就得到了一个正方形,以顶点为标记记作正方形ABCD。
- 从二维到三维:两个平行的正方形ABCD和EFGH可以被连接起来,我们就得到了一个立方体,以顶点标记为立方体ABCDEFGH。
- 从三维到四维:两个平行的立方体ABCDEFGH和IJKLMNOP可以被连接起来,我们于是就得到了一个超正方体,以顶点标记为超正方体ABCDEFGHIJKLMNOP。
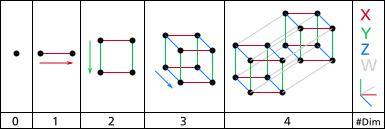 图2.展示如何从点开始得到超正方体的图像
图2.展示如何从点开始得到超正方体的图像
四维方体的结构不易想象,但可以投射至3维或2维空间。在我们将其投影到二维空间中后,把顶点位置调整,可以了解更多。如此获得的图像,不再反映四维方体空间构造,而是反映顶点间的联系。
2.三维投影
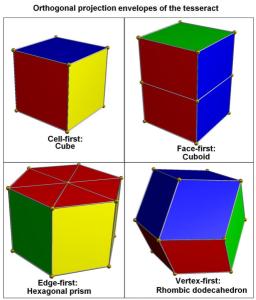 图3.超正方体平行投影的凸包超正方体到三维空间的正对胞的平行投影有一个立方体凸包。最近端的和最远端的胞被投影成了立方体凸包本身,而剩余6个立方体胞则被投影成了立方体的6个正方形面。
图3.超正方体平行投影的凸包超正方体到三维空间的正对胞的平行投影有一个立方体凸包。最近端的和最远端的胞被投影成了立方体凸包本身,而剩余6个立方体胞则被投影成了立方体的6个正方形面。
超正方体到三维空间的正对面的平行投影有一个长方体(正四棱柱)凸包。2对胞被投影成了长方体凸包的上下两半,而剩余4个胞则投影成了正四棱柱凸包的侧面。
超正方体到三维空间的正对棱的平行投影有一个正六棱柱形的凸包。6个胞被投影成了菱形棱柱,它们在正六棱柱凸包中的排列方式就如同立方体正对顶点的平行投影中正方形面投影成的菱形在六边形凸包中的排列方式。剩余的2个胞被投影成了正六棱柱的两个底面。
超正方体到三维空间的正对顶点的平行投影有一个菱形十二面体凸包,事实上,我们正好有两种方法能将菱形十二面体分割成4个全等的平行六面体,因此菱形十二面体中共计有8个全等的平行六面体。超正方体在这种投影下胞的投影就正好是这8个平行六面体。这个投影的体积是超正方体所有投影中最大的。
应用
超级并行/分布计算机是未来一 个时期内计算机的主要发展方向,超立方体是实现其系统 内结 点互连的最具 吸引力的拓扑结构之一。针对超立方体的拓扑结构可在解决通信时间延迟,大幅度提高通信速度的通信技术。
从原理上讲,在这种系统中,任两结点间的通信速度均与结点数无关,原理结构思想是,以6维立方体为基本单元,其中的64个结点连成立方体同时又都连到总线上,连到任一结点的相邻通信通道间均有旁路程控开关,以便在通信中旁路中间结点实现源结点和目的结点间的直通[1]。

-
常染色体隐性遗传性多囊肾
2025-09-28 06:46:06 查看详情 -
奥迪a6cvt更换阀体步骤(奥迪a6cvt更换阀体步骤介绍)
2025-09-28 06:46:06 查看详情 -
长安CS55 瞄向年轻群体/定位A00级市场
2025-09-28 06:46:06 查看详情 -
长安CS75PLUS 瞄向年轻群体/定位A00级市场
2025-09-28 06:46:06 查看详情 -
机电一体化技术专业人才培养方案
2025-09-28 06:46:06 查看详情


 求购
求购






