几何公理系统

从历史的角度看，欧几里得的《几何原本》是两千多年间被公认为用严格的逻辑结构来叙述的科学典范，但用现代数学的严谨要求来看《几何原本》的叙述，显然还有许多不严格的地方。归纳起来，《几何原本》的缺点可以概括为如下几点：第一，有些定义的写法运用了一些它本身就应该定义的概念；第二，有些定义是多余的；第三，在有些定理的证明过程中，依靠了图形的直观，而这种直观自明性又没有列进公理中。

实际上，《几何原本》的这些不足之处，也早就被古代学者所觉察。举个例子，古希腊另一位大数学家阿基米德(Archimedes)仔细研究了欧几里得几何公理系统之后，认为要严格陈述关于长度、面积和体积的测量理论，就必须扩充欧几里得的几何公理系统，如下的一条公理就必须加到欧几里得几何公理系统中去，该公理被后人称为阿基米德公理。

阿基米德公理：任给两个数a>0和b>0，并且ab。

可以用几何图像来陈述如上之阿基米德公理：设AB和CD是任意两个线段，则在直线AB上存在着有限多个点A₁，A₂，A₃，…，A_n-1，A_n，使得A₁在A和A₂之间，A₂在A₁和A₃之间等等。并且线段AA₁，A₁A₂，…，A_n-1A_n都等同于线段CD，而且B在A和A_n之间，如图1所示：

图1

实际上。阿基米德以后的很长历史发展中，人们一直都在努力弥补欧几里得几何公理系统中的缺陷，想方设法完善《几何原本》的陈述。然而一直拖到十九世纪，人们才建立起一个完整的欧几里得几何公理系统。在这个系统中，能够不依靠任何空间直观经验，推出欧几里得几何系统中的所有定理，完成这一艰巨任务的人是德国大数学家希尔伯特(Hilbert)，他为此而出版专著《几何基础》。希尔伯特在这本专著中把几何系统公理化方法推向了完善化阶段，该书被誉为划时代的巨著。

前面指出：欧几里得(Euclid)《几何原本》的陈述，有它逻辑结构上的不足之处，直到19世纪，才由希尔伯特(Hilbert)最终弥补这些不足之处，进而提供了一个完善的Euclid几何公理系统，这一切都写在他的巨著《几何基础》一书中，并由此而解决了用公理方法研究几何学的基础问题。

希尔伯特关于欧几里得几何公理系统的陈述，总体归纳为基本概念和公理两部分。基本概念包括三个基本元素和三个基本关系；公理部分共分为5组，第一组是8条结合公理，第二组有4条顺序公理，第三组是5条合同公理，第四组是2条连续公理，第五组是1条平行公理，这是《几何原本》中的第五公设的等价命题之一。下面我们将希尔伯特陈述欧几里得几何公理系统的结构列表如下^[1]：

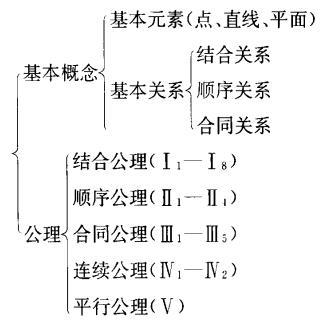图2 几何公理系统的结构

这是Hilbert的经典叙述，而后来，人们已习惯于将连续公理列为第Ⅳ组，平行公理列为第Ⅴ组。另外，又将连续公理中的“完备公理”改为“Cantor公理”，当然，可以证明经过改动后的公理系统与原来的公理系统是等价的，所以这种改动是形式的或非实质的，即在本质上没有对Hilbert所给的Euclid几何公理系统作任何改动。

几何公理系统的解释(interpretation of geometric axiomatic systems)亦称几何公理系统的实现或模型，是几何公理化方法的重要课题。给定一个公理系统∑，为了验证该公理系统的协调性(无矛盾性)，人们往往取现实中存在的一组具体事物M，规定公理系统∑中的每个基本概念对应M中的某一事物，并且验证了：在此规定之下，∑中的每个公理都成立，则M就称为∑的一个解释，或一个实现(模型)，利用这种方法还可以验证公理系统的独立性和完备性。几何公理系统的解释是19世纪中叶随着罗氏几何的产生而发展起来的，贝尔特拉米(E.Beltrami)利用他的微分几何模型，庞加莱(((J.-)H.Poincaré)利用他的复数平面模型，克莱因((C.)F.Klein)利用他的射影几何模型等，各自成功地解释了罗氏几何，模型法已成为研究公理系统的重要方法，特别是当涉及原始概念的对象有无限多时就更是这样。因此，在数学中行之有效的方法是用一种熟知的公理系统A作为新公理系统B的解释，当B为A的子公理系统时，这样做是显然的，如果A协调，显然B也协调；倘若A的协调性尚未确立，则称B具有相对于A的协调性^[2]。

绝对几何公理系统(absolute geometric axiom system)是一种重要的几何公理系统，指在希尔伯特-欧几里得几何系统公理表中去掉平行公理后，所构成的几何公理系统。因此，绝对几何公理系统是由三个基本元素(点、直线、平面)、三个基本关系(结合、顺序、合同)和四组公理(共19条)构成。这四组公理包括：第一组8条结合公理(参见“结合公理”)，第二组4条顺序公理(参见“顺序公理”)，第三组5条合同公理(参见“合同公理”)，第四组2条连续公理(参见“连续公理”)。

几何公理系统的完备性(the completeness of geometric axiom system)是几何公理系统的重要性质，完备性是人们对任何一个公理系统的基本要求之一，而一个几何公理系统的任何两个模型都是同构的(参见下文“几何公理系统模型的同构”)，那么它就满足了完备性要求或称该几何公理系统具有完备性。

先举一例说明一个几何公理系统的两个不同的模型可以是同构的。首先，人们不难在等距面上构造罗巴切夫斯基平面几何公理系统Σ⁰的模型；设σ为罗氏空间中任给一个等距面，而u为σ的底，选定σ上的点和等距线作为客观对象，不难验证所选客观对象之间的关系能满足Σ⁰系统中每一条公理的要求，从而就在σ上构造了一个罗巴切夫斯基平面几何公理系统的模型，现在选取任意两个具有公共底平面u的等距面σ₁和σ₂，然后在σ₁和σ₂上分别构造罗巴切夫斯基平面几何公理系统Σ⁰的两个模型M₁和M₂，现规定，如果σ₁和σ₂上的点位于同一条垂直于底平面u的直线上，则算是互相对应的，如果σ₁和σ₂上等距线位于同一个垂直于u的平面上，则说这两条等距线是互相对应的，则在此对应原则下，Σ⁰的两个不同模型M₁与M₂是同构的。

再举例说明一个公理系统的两个不同模型可以不是同构的，取希尔伯特-欧几里得几何公理表中前三条结合公理Ⅰ₁-Ⅰ₃组成一个独立的几何公理系统(参见“结合公理”)E^A，然后在欧氏空间中任取一个三角形，把该三角形的顶点称为点，把该三角形的边称为直线，因此有了一个共有6个对象(三个点和三条直线)组成的对象系统，记为σ_A，不难验证σ_A的几何元素(即所选之客观对象)间的关系能满足E^A之每一条公理的要求，因而在σ_A上构造了一个E^A的模型M_A，现再在欧氏空间中任取一个四面体，将该四面体之顶点称为点，四面体的棱称为直线，四面体的面称为平面，因此又有了一个计有14个对象构成的对象系统，记为σ_B，容易验证σ_B的几何元素(即所选客观对象)之间的关系同样满足E^A的每一条公理的要求，因而人们又在σ_B上构造了E^A的另一个模型M_B，但在M_A与M_B之间不存在一一对应关系，所以M_A与M_B不是同构的。

完备的公理系统要求它的所有不同模型都是互相同构的.可以严格证明，欧几里得几何公理系统和罗巴切夫斯基几何公理系统都是完备的公理系统。

几何公理系统模型的同构(isomorphism of geometric axiom system model)指对同一几何系统不同模型之间的某种关系的描述，设AX表示由若干个公理所组成的一个公理系统，而AX在两个不同的对象系统Σ^A和Σ^B上分别构造了两个模型M_A和M_B(参见“公理系统的模型”)，如果M_A和M_B的对象之间能够建立这样的一一对应，使得对应元素之间有完全相同的相互关系，则称模型M_A和M_B是同构的。若以几何公理系统之模型对同构概念解释时，就是当某一个几何公理系统之两个不同模型的同名基本对象(如点、直线、平面)之间所构成的一一对应，能够使得在一个模型中由某些基本关系(如连结、在中间、合同等)联系起来的任何一些对象，在另一个模型中必有由相同的关系联系起来的一些对象与之对应。

但应注意，并非同一几何系统的任何两个模型都同构。

欧几里得几何公理系统的相容性(the consistency of Euclidean geometric system)是欧几里得几何公理系统的重要性质。它是关于欧几里得几何公理系统是否相容的讨论与探索，虽说普遍认为欧几里得几何公理系统的相容性是比较信得过的，并对庞加莱模型(即在欧氏几何系统中构造的罗氏几何公理系统的模型)表示出很大兴趣，因为它表征了罗巴切夫斯基几何公理系统的无矛盾性可由欧几里得几何系统的相容性来保证，但也正由此而引起了人们对欧氏几何公理系统之相容性产生怀疑，因为竟然能由之而保证一个包含着相悖于常识之罗氏公设的系统具有相容性，从而促使人们考虑不依靠直觉而在道理上弄明白欧几里得几何公理系统为什么相容，对此，人们受到法国数学家笛卡儿(R.Descartes，)所创立之解析几何的启发，在实数系统中构造了一个欧几里得几何公理系统的模型(参见“笛卡儿模型”)，因此，只要假定实数系统R无矛盾，欧几里得几何公理系统就一定相容，所以庞加莱模型与笛卡儿模型的构造成功表明：只要实数系统R相容，则欧氏几何公理系统与罗氏几何公理系统均为无矛盾系统。